Matematické Fórum

leniczcha · 29. 04. 2012 06:29

Poradí někdo postup, při určování předpisů funkcí z grafu.

vanok · 29. 04. 2012 07:19

↑ leniczcha:
Metoda:
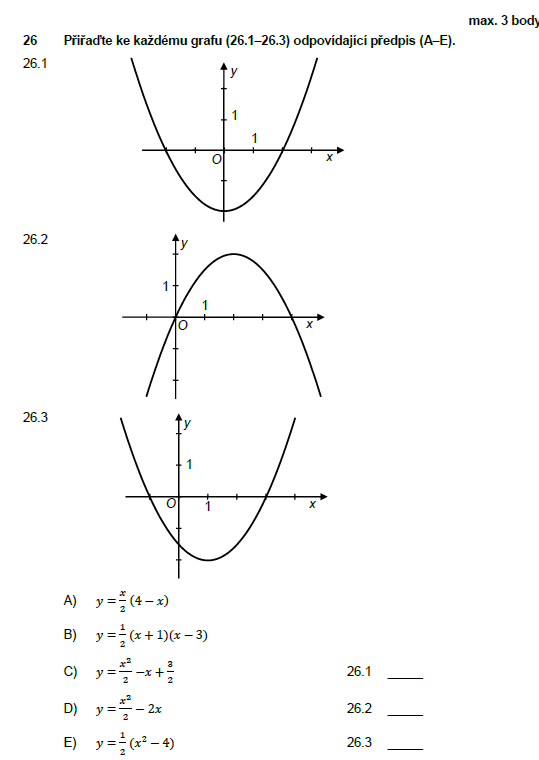
Urci rovnicu kazdej funkcie napriklad vdaka bodom co su na osach ,

napriklad prva funkcia prechadza bodmy (-2,0) (2,0) a (0,-2)
Jej vseobecna rovnica je y=ax^2+bx+c
Dosadenim dostanes jeden system (3,3) a najdes E)

leniczcha · 29. 04. 2012 07:59

Mohla bych poprosit o větší náznak řešení, nejspíš mi vyšel nějaký nesmysl

Bati · 29. 04. 2012 08:18 — Editoval Bati (29. 04. 2012 08:52)

Metoda, kterou popsal vanok je samozřejmě správná, přímočará a obecně platná, ale myslím, že v tomto příkladě zbytečně zdlouhavá (zvlášť pokud by se jednalo o nějaký test na čas). Pokud totiž máme k dispozici 3 grafy a jen 5 odpovědí, půjde nejspíš snadno tipovat a určitě stojí za to si uvědomit pár jednoduchých faktů o kvadratických funkcích :
Jestliže máme přepdis kvadratické funkce $y=ax^2+bx+c\quad a\neq0$ pak platí:

1. Pokud je $a>0$ , pak je funkce konvexní (graf vypadá jako miska), jinak je konkávní (jako kopeček)

2. Pokud 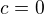$c=0$ , pak graf funkce prochází počátkem souřadnic (neboť má jeden kořen 0)

3. Pokud $a\cdot b<0$ , pak je graf funkce posunutý ve směru osy x (napravo), jinak nalevo a navíc její graf je symetrický podle osy y (uprostřed) právě když $b=0$ .

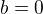Tyto fakty se vyplatí pamatovat a potom lze ten příklad udělat z hlavy vylučovací metodou.

elypsa · 29. 04. 2012 10:42

Případně také velmi rychlá metoda pokud ti nedělá problém počítání z hlavy je ta, že koukneš grafy funkcí a jde si všimnout například toho, že druhá funkce jako jediná prochází bodem [0;0]. Pro jistotu si najdeš ještě jeden bod, který jde vyčíst třeba [4;0]. Tyhle body ([x;y]) dosazuješ do těch rovnic a u které ti to bude sedět, tak ta bude tvoje hledaná.

Takhle bych postupoval u ostatních.

Matematické Fórum

#1 29. 04. 2012 06:29

Předpis funkcí

#2 29. 04. 2012 07:19

Re: Předpis funkcí

#3 29. 04. 2012 07:59

Re: Předpis funkcí

#4 29. 04. 2012 08:18 — Editoval Bati (29. 04. 2012 08:52)

Re: Předpis funkcí

#5 29. 04. 2012 10:42

Re: Předpis funkcí

Zápatí