Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 10. 2008 16:09
Barometrická rovnica
Zdravím,
Dnes pri riešení FKS som narazil na takýto problém: barometrická rovnica hovorí:  . Mám zadaný tlak p_0 a g, ďalej mám zadané, že akúsi fľašu presúvame z výšky 3700 m do 500 m a keďže mám zisti? zmenu objemu pri konštantnej teplote, chcel som z vyššie uvedenej rovnice vypočíta? pomer tlakov vo výške h_1 a h_2. Dostal som sa však len k úprave
. Mám zadaný tlak p_0 a g, ďalej mám zadané, že akúsi fľašu presúvame z výšky 3700 m do 500 m a keďže mám zisti? zmenu objemu pri konštantnej teplote, chcel som z vyššie uvedenej rovnice vypočíta? pomer tlakov vo výške h_1 a h_2. Dostal som sa však len k úprave  . Dá sa z toho nejak vyjadri? pomer
. Dá sa z toho nejak vyjadri? pomer  ?
?
You know who
(or maybe not)
Offline
#2 12. 10. 2008 09:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Barometrická rovnica
Zdravím:-)
pokud bych potřebovala poměr p_1/p_2, tak bych postupovala takto: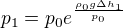
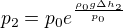
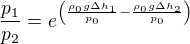
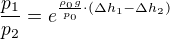


Zda to má souvislost se samotným postupem řešení, to jsem moc podrobně nezkoumala, ale na to se neptáš :-)
Hodně zdaru :-)
Offline
#3 12. 10. 2008 11:44
Re: Barometrická rovnica
tenot pomer  som síce dostal tiež, ale tam musím vedie? hustotu rho_0 a tá nie je zadaná. Uvažoval som pri riešení takto: Platí stavová rovnica, tj.
som síce dostal tiež, ale tam musím vedie? hustotu rho_0 a tá nie je zadaná. Uvažoval som pri riešení takto: Platí stavová rovnica, tj. 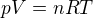 , len v tejto rovnici mám akosi furt 2 neznáme a ani jednu sa mi zo zadaných hodnôt nepodarilo dopočíta?.
, len v tejto rovnici mám akosi furt 2 neznáme a ani jednu sa mi zo zadaných hodnôt nepodarilo dopočíta?.
You know who
(or maybe not)
Offline
#4 12. 10. 2008 14:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Barometrická rovnica
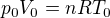
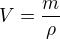 ,
,  a platí zákon zachování hmotnosti, pomůže to?
a platí zákon zachování hmotnosti, pomůže to?
Teď se postupně přesouvám z Vysočiny přes Brno (odkud se hlásím :-) až do Opavy, další reakce až večer :-)
Offline
#5 12. 10. 2008 17:45
Re: Barometrická rovnica
Hmm...
Ale v tých rovniciach mám stále len dve neznáme nie? Aj keď ich posájam (porovnám cez m, vyjadrím n a dosadím za n do stavovej rovnice). Mám zadané len M_r, V, R, T. A to, že platí zákon zachovania hmotnosti v podstate hovorí, že sa nemení n a keďže sa nemení ani T tak že P_0.V_0=konst, nie? No z toho sa aj tak neveim dopátra? k výsledku.
You know who
(or maybe not)
Offline
#6 12. 10. 2008 22:18 — Editoval rughar (12. 10. 2008 22:20)
Re: Barometrická rovnica
Příklad je bez znalosti hustoty vzduchu při zemském povrchu zcela určitě neřešitelný. Ten vzorec co tam je napsaný popisuje izotermickou atmosféru. Takto by vypadal průběh tlaku, pokud by byla všude stejná teplota (silně nerealistické, ale to nechme stranou). Můžeš si představit, že máš atmosféru, kde při zemi je tlak p0. Teď si představ takovou, kde je dvojnásobná teplota. Tlak se těsně u země žádným způsobem nezmění (hmotnost vzduchu nad tvojí hlavou je stále stejná). Avšak vzduch se více rozpíná a tak tlak klesá pomaleji. Tím pádem jsem dostal dvě různé atmosféry o stejném tlaku p0, ale různém tlaku v nějaké konkrétní výšce. Čili musíš znát buď tu hustotu a nebo alespoň teplotu. Pokud bys znal teplotu, tak to vyřešíš tím posledním, co psala jelena.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#7 12. 10. 2008 22:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Barometrická rovnica
↑ rughar:
Zdravím :-)
Zadaní počítá s konstatntní teplotou - což je silně nerealistické :-) http://www.fks.sk/archiv/2008_09/24zadAB1_sk.pdf - kolega matoxy umístil odkaz na zadání do 1. zprávy v tomto tématu. S ohledem na zadání je můj návod OK?
Pro kolegu matoxy:
Sice se mi nelibí v zadání pojem "typicky atmosferický tlak", ale předpokládám, že tak říkaji p_0.
Doporučuji: http://en.wikipedia.org/wiki/Internatio … Atmosphere
Offline
#8 12. 10. 2008 23:09 — Editoval rughar (12. 10. 2008 23:27)
Re: Barometrická rovnica
↑ jelena:
Aha. Tak v tom případě i tak máš samozřejmě pravdu. Já bych to teda popsal (po přečtení skutečného zadání) takto
p V = N*k*T
Z tohoto vztahu jde přesně vytáhnout rozdíl objemů. Konstanty mě nemusí vůbec zajímat. Právě totiž přesně tolikrát, kolikrát je menší teplota (v kelvinech), tolikrát se zmenší objem. A jestli se nemýlím, tak právě rozdíl teplot je dán, takže změna objemu je pak jasná. Žádné další znalosti o atmosféře (jestli je adiabatická, izotermická nebo kdoví jaká) nejsou potřeba.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#9 13. 10. 2008 09:10 — Editoval matoxy (13. 10. 2008 09:36)
Re: Barometrická rovnica
Tak nakoniec som počítal takto: 
Keď už máme hustotu počítame Tlak p_1 podľa tej barometrickej rovnice a potom len dosadím do stavovej rovnice.
EDITACE: napísal som sem na čas aj výsledok lebo som to potreboval napísa? do riešenia, ale nie je tu MicrosoftEquation. Keďže sa dá však ešte dnes odovzdáva?, radčšej som výsledok vymazal (ak by bol náhodou správny).
Inak (stačí ak napíšete aj zajtra) je takýto postup správny?
You know who
(or maybe not)
Offline
#10 13. 10. 2008 19:50 — Editoval rughar (13. 10. 2008 20:27)
Re: Barometrická rovnica
↑ matoxy:
Tak ještě trochu jinak. Začal bych možná od začátku. U Země mi vzduch disponuje nějakým p0 a T0. V horách je to p1 a T1. Objem flašky v nížině bude V0 a na horách V1. V zadání se ptají na změnu objemu, takže nebudeme řešit hustotu, ale objem. V rámci lahve se zavhovává množství vzduchu uvnitř. Takže ze stavové rovnice, kde víme že objem bude úměrný teplotě a nepřímo úměrný tlaku můžeme vyjádřit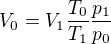
Obě teploty jsou jasně dány, takže jediný problém který zůstává, je tlak. Jedna možná interpretace je považovat jej všude zakonstantní. V každém případě pokud budeme odvozovat vztah pro tlak, tak je nesmysl uvažovat vzorec pro izotermickou atmosféru a zároveň počítat s tím, že se změna teplot projeví na změně objemu. Správnějším modelem by byla adiabatická atmosféra. U ní víme, že každý element vzduchu o konstantním n splňuje
Naše rovnice pro změnu objemu pak bude vypadat takto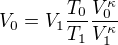
po úpravě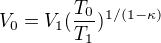
Inu. Pro kappa rovno 1 nemá rovnice smysl. Kappa = 1 totiž odpovídá tomu, že se zachovává teplota s rozdílnou výškou, což už není pravda ze zadání. Velmi rád bych provedl nějaké zjevné omezení, ale to zkrátka nejde. To, jak se mění objem zkrátka velmi přímo závisí na hodnotě kappa. Je vidět, že pro různé její hodnoty dostaneme dost odlišné výsledky. Mimochodem ještě jsem neřekl co to je. Je to Poissonova konstanta a je popsaná takto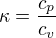
cp je měrná tepelná kapacita ovzduší při konstatním tlaku a cv při konstantním objemu. Podle této definice je pak kappa vždy větší nebo rovno než 1. Většinou se pohybuje mezi hodnotami 1,3 .. 1,6.
Po Editaci: O příspěvek dříve jsem uváděl, že nezáleží na povaze atmosféry. To jsem se ale šeredně spletl. Je těžká hloupost uvažovat, že tlak je konstantní. Pokud je nezanedbatelný poměr teplot, tak je vždy nezanedbatelný i poměr tlaků. Takže konstantní tlak zkrátka nelze uvažovat když neuvažujeme konstantní teplotu. To už má větší smysl uvažovat konstantní teplotu před konstatním tlakem. A to nemůžeme už z principu úlohy (to by se zachovávlo uplně všechno i proti zadaným hodnotám a objem flašky by se neměnil).
Po další editaci: Pokud přecejen bude uvažován konstantní tlak a různá tepltota (stále nevim jak dát dostatečně najevo, že to je ale nehorázná hloupost), takby řešení plynulo přímo ze stavové rovnice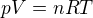
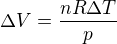
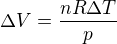
Molární množství molekul vzduchu pak spočítáš, když budeš znát jeho hmotnost uvnitř lahve. K tomu si určíš hodnotu hustoty vzduchu (dusíku). Tu už si spočetl tak dosadíš. Ale znova varuji že tento postup je trestuhodný :-)
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#11 14. 10. 2008 12:41
Re: Barometrická rovnica
Rughar, k tej poslednej editácii tvojho príspevku: ale stále je problém je v tom, že máme priveľa neznámych - n, \Delta V, hustota, tlak. A okrem tej rovnice ktorú som uviedol vyššie som neprišiel na to, ako pospája? rovnice, aby sa to dalo rieši?.
You know who
(or maybe not)
Offline
#12 14. 10. 2008 14:12 — Editoval rughar (14. 10. 2008 14:12)
Re: Barometrická rovnica
↑ matoxy:
No tak v té poslední mám jako neznámou objem. Ten chci spočítat. Takže je tam ještě molární množství. To si můžu vyjádřit jako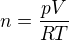
S tím, že dosadím počáteční hodnoty a také původním objem flašky. Takže hustota zase potřeba ani není.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#13 15. 10. 2008 09:09
Re: Barometrická rovnica
Ale v zadaní príkladu nie je zadaný počiatočný tlak, ale tlak p_0, čiže tlak, ktorý ak som dobre pochopil, je tlak vo výške h=0m.
A ak chceme dopočíta? tlak v nejakej výške potrebujeme hustotu vzduchu. A aj ak by sme predpokladali, že je atmosféra len z dusíka, len z jeho molovej hmotnosi a objemu nedopočítame jeho hustotu nie?
You know who
(or maybe not)
Offline
#14 17. 10. 2008 20:38
Re: Barometrická rovnica
Pouze pokud uvažuju konstantní tlak, pak je to mé řešení po editaci správně. Pokud neuvažuju konstantní tlak a zároveň neuvažuju ani konstantní teplotu, pak se nedá nic dělat, ale atmosféra není ani izotermická ani izobarická no a nějaká být zkrátka musí, takže už zbyla jen adiabatická (atmosféru s konstantní hustotou rovnou zavrhuju, úkol by přestával dávat smysl, z flaškou by se nic nestalo). A to jak už jsem odvodil, tak vede na řešení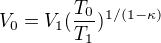
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#15 18. 10. 2008 00:54 — Editoval BrozekP (18. 10. 2008 01:02)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Barometrická rovnica
Není mi moc jasné, co tu vlastně řešíte (možná to je tím, že jsem nepozorně četl), ale přijde mi to jako jasná úloha na použití barometrické rovnice (případně s jejím odvozením). Řešení pak vypadá takto:
Vzhledem k tomu, že máme uvažovat stálou teplotu 20°C, tak pro vzduch ve flašce platí ze stavové rovnice ideálního plynu 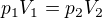 a tedy
a tedy 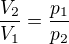 . Flaška je lehce deformovatelná, tlak uvnitř flašky bude tedy vždy stejný jako tlak okolí. Zkoumejme tedy tlak atmosféry. Pro přírůstek tlaku zřejmě platí
. Flaška je lehce deformovatelná, tlak uvnitř flašky bude tedy vždy stejný jako tlak okolí. Zkoumejme tedy tlak atmosféry. Pro přírůstek tlaku zřejmě platí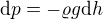 (dostaneme například porovnáním tlakových sil a gravitační síly na elementární krychli vzduchu)
(dostaneme například porovnáním tlakových sil a gravitační síly na elementární krychli vzduchu)
Ze stavové rovnice ideálního plynu si vyjádříme hustotu
a dosadíme
Atmosféru dále považuji za izotermickou, nezpůsobí to příliš velkou chybu. To znamená, že teplota není funkcí ani tlaku ani výšky, označím ji 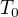 . Máme tedy separované proměnné, takže integrujeme, určíme integrační konstantu a nakonec dostaneme
. Máme tedy separované proměnné, takže integrujeme, určíme integrační konstantu a nakonec dostaneme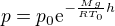 .
.
Platí tedy
Máme tak
Pro adiabatickou atmosféru:
Podle Poissonova zákona (jestliže hodnoty s indexem nula jsou hodnoty v h=0)
a tedy
Separujeme proměnné a integrujeme
Snadno zjistíme, že 
Vyjádříme tlak a upravíme: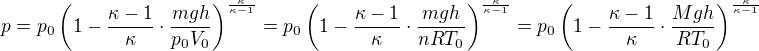
Pro 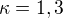 tak máme
tak máme
Pro zadané hodnoty a uvedené modely atmosfér uvedu graf závislosti tlaku v pascalech na výšce v metrech.
Svislá čára značí výšku 3700m.
Modrá křivka je graf pro izotermickou atmosféru.
Fialová křivka je graf pro adiabatickou atmosféru s 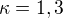
Zelená křivka je graf pro adiabatickou atmosféru s 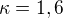

Je tedy vidět, že pro přibližný odhad v malých výškách je dostatečně dobrý model izotermické atmosféry. Rozdíl oproti adiabatické je minimální a s izotermickou jsou jednodušší výpočty.
Offline
#16 18. 10. 2008 12:16 — Editoval rughar (18. 10. 2008 12:17)
Re: Barometrická rovnica
↑ BrozekP:
Aaaa. Jsem roura. Kdo řekl, že se teplota nějak mění? Vždy? v zadání to není. Já jsem celou dobu pracoval s tím, že jsou ty teploty rozdílné, tak jsem považoval za hloupost izotermickou atmosféru. Omlouvám se tím pádem za mé příspěvky. Do jednoho byla jejich souvislost z úkolem naprosto nulová :-). Tvé řešení s použitím izotermické atmosféry je tedy dobře. Lze využít i zjednodušeného vztahu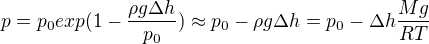
který je znám i středoškolákům. Výjde to prakticky stejně. Ta adiabatická atmosféra je tedy (jelikož se podle zadání nemění teplota) zcela mimo.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#17 18. 10. 2008 12:39
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Barometrická rovnica
↑ rughar:
Ta adiabatická by měla smysl, pokud bychom to chápali tak, že flašku budeme mít při konstantní teplotě (objemy budeme např. zjiš?ovat v obou případech v místnosti vytápěné na 20°C). Teplota atmosféry může být v různých výškách různá, ale teplota flašky bude stejná.
Offline
#18 29. 10. 2008 12:21 — Editoval matoxy (29. 10. 2008 12:21)
Re: Barometrická rovnica
Zdravím,
dlhšie som sa neozval, lebo som bol mimo Slovenska, ale nakoniec som ten príklad vypočítal až na malú numerickú chybu dobre, keď som si uvedomil, že platí:  a potom už stačilo dosadi? do tej barometrickej rovnice. Ďakujem za pomoc.
a potom už stačilo dosadi? do tej barometrickej rovnice. Ďakujem za pomoc.
You know who
(or maybe not)
Offline