Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Geometrická posloupnost: soustava (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 05. 2012 11:01
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
Geometrická posloupnost: soustava
Ahoj,
mám určit: 
a je dáno:

Vyjádřila jsem si všechny členy pomocí prvního členu, získala tak soustavu rovnic o dvou neznámých.
Zvolila jsem při řešení dosazovací metodu.
A vychází mi rovnice, ve které nevím, jak se zbavit třetí mocniny, abych mohla dál třeba řešit pouze kvadratickou rovnici...
Vyšlo mi např. 
Už vidím - rozložím si: 
- zkrátím co se dá
- vznikne mi kvadratická rovnice: 
A výsledné kvocienty se mi nějak nezdají...
Mohl by prosím někdo pomoct s řešením, najít případně chybu?
Výsledek mi není znám, takže není ani podle čeho kontrolovat .-/
Díky.
Offline
- (téma jako vyřešené označil(a) Kouří se mi v hlavě)
#2 05. 05. 2012 11:21
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Geometrická posloupnost: soustava
↑ Kouří se mi v hlavě:
Až tady potaď  dobře potom:
dobře potom:
Nikdo není dokonalý
Offline
#4 05. 05. 2012 11:28
#5 05. 05. 2012 11:37 — Editoval elypsa (05. 05. 2012 11:38)
Re: Geometrická posloupnost: soustava
↑ Kouří se mi v hlavě:
"Minimálně" se zdokonalíš a udělá pár lidí šťastnější, že jim pomůže. Když se podívám například na sebe tak aktivně to tu navštěvuji(vlastně každý den), asi tak od listopadu minulého roku. A pokud se podívám na svou matematiku před listopadem a teď, tak to je úplně něco jiného :). Zdejší lidi dokážou motivovat a pomoc velmi dobře.
Měj se.
Baf!
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Geometrická posloupnost: soustava (TOTO TÉMA JE VYŘEŠENÉ)


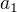 to by mě nenapadlo, jak elegantní!
to by mě nenapadlo, jak elegantní!