Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
#1 05. 05. 2012 22:19
Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
Ahojte ,
Neviete mi niekto prosim vas pomoct s 1 prikladom s ktorym si neviem rady?
Zadanie znie : Mame pravidelny Sestuholnik s bodmi ABCDEF pricom
A = (0,0)
B=(1,0)
C=(3/2,(odmocnina z 3)/2)
mame zistit
F =
E=
D=
viemi niekto pomoct? aspon ukazat ako vypocitam 1 bod aby som vedel ako dopocitat ostatne
Offline
#2 06. 05. 2012 10:53
Re: Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
Ahoj ↑ Miox:,
Metoda:
Najdi stred S trojuholnika ABC (vsetko kresli)
Na urcenie chybajucych bodom vyuzi symetrie pravidelneho sestuholnika.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 06. 05. 2012 20:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
↑ Miox:
Zdravím,
pokud ještě aktuální - využila bych, že body A, B jsou na ose x. Pomocí osové symetrie víme, že body D, E budou mít stejné x-souřadnice. Potom víme, že bod F bude mít stejnou y-souřadnici jako bod C a osa úsečky AB bude osou symetrie pro zobrazení C->F.
Také víme délku strany šestiúhelníku (|AB|=1 jednotka). To už by mělo stačit na dořešení (snad).
Offline
#5 07. 05. 2012 22:52
Re: Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
tak dosiel som na to ze vlastne v prav sestuholniku je AB vlastne polomer . toto vyuzijem na to ze spravim z ab vektor = b-a , a potom viem ze
r=(b-a)
C + 2*(b-a) = F
potom uz viem spravit vektor CF = F-C z neho spravim kolmy vektor a ten kolmy vektor uz iba dopocitavam s bodmi takto
A+normalovy vektor F-C =E
B + normalovy vektor F-C = D
da sa to tak pocitat alebo je este neico jednoduchsie?
Offline
#6 07. 05. 2012 23:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
↑ Miox:
asi bych počítala jen pomocí vzdálenosti - jednu souřadnici každého bodu znám, vzdálenost do některého sousedního bodu (jehož souřadnice komplet znám) také, tedy pomocí vzorce pro vzdálenost bodů dopočtu 2. souřadnici.
Co myslíš? Děkuji.
Offline
#7 08. 05. 2012 09:11
Re: Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
Dobrý den.
Myslím, že nejjednodušší metodou je pouhé posouvání bodů o vektory.
Víme, že úsečka AD je rovnoběžná s úsečkou BC. Z vlastností prav. šestiúhelníku dále plyne, že |AD|=2|BC|.
Souřadnice bodu D tedy získáme tak, že bod A posuneme o dva vektory C-B.
Souřadnice bodu E získáme posunutím bodu D o vektor A-B.
Analogicky zjistíme i souřadnice bodu F.
Offline
#8 08. 05. 2012 15:23
Re: Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
a podla osovej sumernosti sa to neda?
neviem vobec ako to jelena myslis s tym vypocitanim , mohla by si mi to napisat pls
a este by som sa vas chcel spytat ked mam niaky bod napr
A ( 19,-1) a S ( 5,-1) mam spavit ze do akeho bodu to spravi ta osova sumernost tak ako to vypocitam? dakujem
Offline
#9 08. 05. 2012 16:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C
↑ Miox:
Myslela jsem, že znám vzdálenost jednotlivých sousedních vrcholů - jako délku úsečky |AB|=1. Bod D má souřadnice [1, y] a platí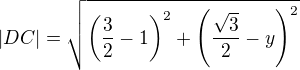 
, 
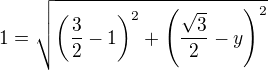dle vzorce pro vzdálenost bodů. Dopočtu y.
Od kolegů máš i další užitečné rady, děkuji, určitě se podaří dořešit.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analyticka GEO , vypocet bodov v prav sestuholniku ked vieme A,B,C