Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
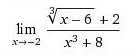
.![$A=\sqrt[3]{x-6}\quad B=2$](/mathtex/a3/a368d309179e7e8cd66ca40271b06aa9.gif "kopírovat do textarea")
a rozšířit zlomek tak, abys v čitateli dostala to ![$A^3+B^3=(A+B)(A^2-AB+B^2)\\
(\sqrt[3]{x-6})^3+2^3=(\sqrt[3]{x-6}+2)((\sqrt[3]{x-6})^2-2\sqrt[3]{x-6}+2^2)\\
x+2=\underbrace{(\sqrt[3]{x-6}+2)}_{\text{čitatel limity}}\underbrace{((\sqrt[3]{x-6})^2-2\sqrt[3]{x-6}+4)}_{\text{výraz, kterým je potřeba rozšířit}}$](/mathtex/70/7094a47481f2765b3381ee0f34766215.gif "kopírovat do textarea")
![$\lim_{x\to-2}\frac{\sqrt[3]{x-6}+2}{x^3{}}.\frac{\sqrt[3]{(x-6)^{2}}-2\sqrt[3]{x-6}+4}{\sqrt[3]{(
x-6)^{2}}-2\sqrt[3]{x-6}+4}$](/mathtex/22/22bc1132ae66c4a9ffea7c41b838b754.gif "kopírovat do textarea")
![$=\lim_{x\to-2}\frac{x-6+8}{(x+2)(x^2-2x+4){}}.\frac{1}{\sqrt[3]{(
x-6)^{2}}-2\sqrt[3]{x-6}+4}$](/mathtex/3d/3d9439970d78e7450a1e13d2d15d8bec.gif "kopírovat do textarea")
![$\sqrt[3]{-2-6}$](/mathtex/1f/1fa2084f6ed1406bcfc188ebc70abf5c.gif "kopírovat do textarea")
- když pod odmocninou nesmí být záporné číslo:-(![$\lim_{x\to-2}\frac{1}{(x^{2}-2x+4).(\sqrt[3]{(x-6)^{2}}-2\sqrt[3]{x-6}+4}$](/mathtex/ad/ad33c132b92026815b2c24858d48c228.gif "kopírovat do textarea")
#13 10. 05. 2012 20:43
Offline