Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 11. 2008 22:14 — Editoval matoxy (01. 11. 2008 22:15)
Šikmí vrh
Pekný večer,
nedávno som narazil na takýto príklad: Cieľ leži v šikmej vzdialenosti d=6000m pod polohovým uhlom fí=30 stupňov. Aká musí by? minimálna počiatočná rýchlos?strely,aby bol cieľ zasiahnutý? aký elevačný uhol odpoveda tejto rýchlosti?
Počítal som takto: Z polohového uhla som si určil výšku cieľa a jeho vzdialenos? od bodu výstrelu. Dostal som teda x-ovúv a y-ovú súradnicu cieľa. Skúšal som výs? z rovníc pre polohu projektilu vo vákuu ak poznáme čas letu elevačný uhol a počiatočnú rýchlos?, avšak to mám dve rovnice o troch neznámych. Inštinkt mi však hovorí, že ten čas by mal nejak závysie? na počiatočnej rýchlosti a elevačnom uhle.
Nevedel by niekto nejaký nápad?
You know who
(or maybe not)
Offline
#2 02. 11. 2008 00:42 — Editoval rughar (02. 11. 2008 01:03)
Re: Šikmí vrh
↑ matoxy:
Co třeba vzít cíl a kanón a těmato dvěma body proložit osu x? Osa y bude kolmá. Pak se to malinko zjednoduší. Akorát gravitační zrychlení nebude mířit přímo dolů, ale trochu šikmo. Rovnice v těchto souřadnicích pak budou vypadat takto.



Úhlem beta si označím úhel, který bude svírat vektor počáteční rychlosti s naší osou x. Pak bude platit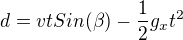

v představuje velikost rychlosti. Z druhé rovnice můžeme velmi jednoduše vyjádřit čas (jedním je t = 0, ale ten nás nezajímá)
Dosadíme do první rovnice a dostáváme
Po úpravě
Nyní se snažíme volit takovou hodnotu beta, aby hodnota v byla minimální. Můžeme dál psát

Tato podmínka je splněna, pokud
Extrémy funkcí se hladají metdou nulové derivace. Zderivujeme výraz jako funkci závislou na beta a následně derivaci položíme rovnu nule.


Řešením je tedy zjevně
Tím je vyřešen úhel. k výpočtu rychlosti můžeme využít vztah, ke kterému jsme došli někde v půli cesty
Můžeme ještě pro úplné vyjádření dosadit za hodnotu úhlo beta

1 + 1 = 1 + 1
... a nebo taky ne
Offline