Matematické Fórum

etchie · 23. 05. 2012 21:17 — Editoval etchie (23. 05. 2012 21:48)

Ahojte,

odhad chyby pri počítaní numerického integrálu pomocou Simpsonovej metódy vyzerá takto:

$|\varepsilon|\le\frac{(b-a)^5}{180n^4}M_4$

pričom $M_4=max|f^{(4)}(x)|$ pre $x\in <a,b>$

zo vzorca pre chybu si vyjadrím n aby som vedel ako mám rozdeliť interval <a,b> pre požadovanú presnosť epsilon.
Problém je, že štvrtá derivácia väčšiny normálnych funkcií je 0. čiže potom aj M4 = 0.
následne dostávam že potrebujem počet delení 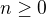$n \ge 0$ , čo mi teda nijako nepomôže, lebo to som "tušil" aj bez vzorca.
ako sa správne používa táto metóda a hlavne ako sa stanoví nejaké zmysluplné n ?

ďakujem pekne za odpovede

jarrro · 23. 05. 2012 21:41

štrvrtá derivácia je identicky na intervale nulová len pre polynómy najviac tretieho stupňa
$f^{$4$}{$x$}=0\nl f^{\prime\prime\prime}{$x$}=a\nl f^{\prime\prime}{$x$}=ax+b\nl f^{\prime}{$x$}=\frac{ax^2}{2}+bx+c\nl f{$x$}=\frac{ax^3}{6}+\frac{bx^2}{2}+cx+d$ teda pre takéto polynómy je Simpsonova metóda úplne presná, teda má nulovú chybu, ale takéto srandovné funkcie sa dajú pekne integrovať aj priamo

etchie · 23. 05. 2012 21:57

↑ jarrro:

z toho mi vyplýva, že ak M4=0, tak potom n musí byť 2, pretože podmenka Simpsonovej metódy je párne n. pričom dostávam presné riešenie s najmenším možným n. toto som skúšal pre počítanie obsahu pod parabolou a sedelo to presne. teraz skúšam jednoduchšiu verziu a počítam obsah pod lineárnou funkciou. a tu mi to nesedí presne. mám tam odchýlku aj pre veľké hodnoty ako n = 100. čo ale bude asi znamenať, že mám chybu vo svojom výpočte (programe).

etchie · 23. 05. 2012 22:45

no je to tak ako som písal, chyba vo výpočte.

vzorec pre výpočet začína s delením intervalu od x0 cez x1 až po xn.
krajné funkčné hodnoty sa sumujú iba raz, párne 2x a nepárne 4x. takto to mám zafixované v hlave.

ale keď sa vzorec prepíše do programovacieho jazyka, ktorý indexuje polia od 1 (Matlab), tak preč je všetka párnosť aj nepárnosť zo vzorca. v Matlabe pri absencii indexu 0 je všetko ohľadom párnosti a nepárnosti naopak. je to posunuté o 1 a takáto chyba je doslova neviditeľná.

ďakujem za pomoc.

jarrro · 23. 05. 2012 22:51

↑ etchie:wolfram potvrdzuje správnosť Simpsona pre polynómy najviac tretieho stupňa

Matematické Fórum

#1 23. 05. 2012 21:17 — Editoval etchie (23. 05. 2012 21:48)

Simpsonova metóda - numerický integrál

#2 23. 05. 2012 21:41

Re: Simpsonova metóda - numerický integrál

#3 23. 05. 2012 21:57

Re: Simpsonova metóda - numerický integrál

#4 23. 05. 2012 22:45

Re: Simpsonova metóda - numerický integrál

#5 23. 05. 2012 22:51

Re: Simpsonova metóda - numerický integrál

Zápatí