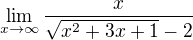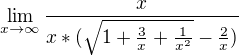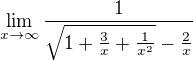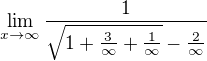Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 11. 2008 20:38
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
limita funkce
Ahoj, mám problém
Vypočítejte  , kde
, kde
f(x)=

kdyby to někdo vypočítal a napsal kolik vyšlo byla bych strašně ráda. dík
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#3 03. 11. 2008 21:43 — Editoval gladiator01 (03. 11. 2008 21:56)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: limita funkce
ve skriptech je totiž ve výsledcích pro +nekonečno -1 a pro -nekonečno 1 (je možné, že to je špatně, překlep-těch tam je hromadu). já bych to taky takhle spočítala (jako ty) já se jen chtěla ujistit, že mam pravdu.
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#4 03. 11. 2008 22:05
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: limita funkce
↑ gladiator01:Frantík to počítal jen pro +oo, pro -oo to vyjde opravdu -1 (postup stejný, až na to, že před odmocninu vytýkáme |x|=-x).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 03. 11. 2008 22:10
Re: limita funkce
↑ gladiator01:
myslím, že to má být takhle, vytknu x, ale to musí být v absolutní hodnotě,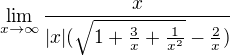
proto ted budu rozlišovat zda x je kladne, ci zaporne
vyraz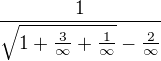
protože vyraz pod odmocninou jde limitně(pro minus is plus nekonečno) k +1
je pro x zaporna -1
a pro x kladna +1 takže
podle mě
Offline
#6 03. 11. 2008 22:23 — Editoval gladiator01 (03. 11. 2008 22:24)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: limita funkce
↑ dr.dracek:
díky, taky myslím
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#7 03. 11. 2008 22:27
Offline
#8 04. 11. 2008 08:28
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1268
- Reputace: 19
- Web
Re: limita funkce
↑ dr.dracek:
Souhlas
Offline