Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Ukážkový príklad na ústnu maturitu na Slovensku č.3 (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 05. 2012 14:14
Ukážkový príklad na ústnu maturitu na Slovensku č.3
4. Dokážte, že dané body A(2,1,6) B (0,-1,-6) a C(-1,2,0) a)určujú rovinu b) napíšte jej rovnicu c)vypočítajte súradnice bodov, v ktorých rovina pretína osi x,y,z.
1) Aby určovaly body rovinu, nesmí ležet na jedné přímce
2) napíšeš rovnici roviny - to snad ze tří bodů umíš
3) Aby jsi našla průsečík s osou x, tak za y a z dosadíš nulu, jelikož bod na ose x má souřadnice x;0;0. Podobně pro další průsečíky
Tomuto nerozumiem vôbec :( Prosím vysvetlite mi to detailne. Vopred dakujem.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 23. 05. 2012 16:56
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Ukážkový príklad na ústnu maturitu na Slovensku č.3
↑ mju:
1) Vektory AB = (-2, -2, -12), AC= (-3, 1, -6), BC = (-1, 3, 6)
pokud by body ležely v jedné přímce, tak vektory by byly navzájem násobky, což v tomto případě nejsou, proto body určují rovinu.
2) Pro parametrické vyjádření stačí zadat jeden bod a dva směrové vektory. Například vezmu bod A a vektory AB a BC.
x = 2 - 2t - s
y = 1 - 2t + 3s
z = 6 - 12t + 6s
3) Zvládneš to už sama?
Průsečík s osou x: dosaď za y,z nuly, takže budeš mít soustavu tří rovnic o třech neznámých (x, t, s)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 23. 05. 2012 17:34
Re: Ukážkový príklad na ústnu maturitu na Slovensku č.3
↑ Aquabellla: Ďakujem veľmi pekne. Už tomu rozumiem :)
Offline
#4 24. 05. 2012 14:16
Re: Ukážkový príklad na ústnu maturitu na Slovensku č.3
↑ Aquabellla: to po c) ma ešte trápi. dosadila som si za y a z 0 a dostala som vlastne x= 9-16 . t +8 . s...Čo dalej s tým? Ako stade zistím tie súradnice? čo mám kam doplniť.
Offline
#5 24. 05. 2012 14:47
Re: Ukážkový príklad na ústnu maturitu na Slovensku č.3
↑ mju:
Dosadíš 0 za y a z
Ty dolní dvě rovnice vyřešíš jako klasické rovnice o dvou neznámých a do rovnice X dosadíš vypočtené S a T. Poté by ti průsečík s osou X měl vyjít
Pokud jsem Vám pomohl vyřešit příklad, dejte prosím palec :)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Ukážkový príklad na ústnu maturitu na Slovensku č.3 (TOTO TÉMA JE VYŘEŠENÉ)





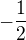 a s=
a s=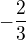 a po dosadený to tej x-ovej rovnice som dostala že x=4.
a po dosadený to tej x-ovej rovnice som dostala že x=4.