Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 05. 2012 20:38
Re: komplexni cisla
Ahoj,
stačí zapsat i v goniometrickém tvaru a pak použít vzorec pro násobení čísel v goniom. tvaru.
Lidé se dělí do 10 skupin. Na ty, kdo rozumějí binárnímu kódu, na ty, kdo mu nerozumějí, a na ty, kdo si myslí, že tohle je vtip o binárním kódu ;)
Offline
#4 27. 05. 2012 21:00
Re: komplexni cisla
Tak  se dá zapsat v goniometrickém tvaru stejně jako každé jiné komplexní číslo.
se dá zapsat v goniometrickém tvaru stejně jako každé jiné komplexní číslo.
Pak použij vzorec pro násobení komplexních čísel v goniometrickém tvaru, pokud jste se ho učili ovšem:
kde 
Už je to lepší?
Lidé se dělí do 10 skupin. Na ty, kdo rozumějí binárnímu kódu, na ty, kdo mu nerozumějí, a na ty, kdo si myslí, že tohle je vtip o binárním kódu ;)
Offline
#5 27. 05. 2012 21:16 — Editoval vanok (27. 05. 2012 21:19)
Re: komplexni cisla
Poznamka, na riesenie mozes pouzit tieto zname vzorce:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

![kopírovat do textarea $z=3i[cos(\frac{1}{4}\pi) +isin(\frac{1}{4}\pi )]^{3}$](/mathtex/57/57c1bb05650b5f3d44463990b2a4c40d.gif)
![kopírovat do textarea $z=3i[cos(\frac{3}{4}\pi) +isin(\frac{3}{4}\pi )]$](/mathtex/b3/b30af0ab41d094f02b0bedd1806474e9.gif)
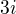
![kopírovat do textarea $z=3[cos(\frac{5}{4}\pi) +isin(\frac{5}{4}\pi )]$](/mathtex/ed/ed2cfc24a2cde7efb6185191270da4b8.gif)
