Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
![kopírovat do textarea $y=(12\sqrt{x^{3}\sqrt{x}})/(5\sqrt[3]{x^{4}})$](/mathtex/5c/5c68e4d393397f392c5c0d902da14965.gif)
![kopírovat do textarea $y=1/\sqrt[12]{x^{7}}$](/mathtex/d0/d0ff56916a15b47c7db239607b68883f.gif)
![kopírovat do textarea $\sqrt[n]{x^m}=x^{\frac{m}{n}}$](/mathtex/74/74ab46aa2a39cd02e3c0dee08c00d55f.gif)
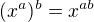
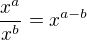

![kopírovat do textarea $12/5*[x^{(3/2)*(1/3)}/x^{4/3}]$](/mathtex/34/34f71ce4a2bd7575295797b3cab49d57.gif)