Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Extrémy implicitní funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 06. 2012 20:20
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Extrémy implicitní funkce
Pěkný večer přeji.
Určete lokální extrémy funkce  určené implicitně rovnicí
určené implicitně rovnicí  .
.
Derivace podle x: =>
=>  =>
=> 
Derivace podle y: =>
=>  =>
=> 
Mám dvě rovnice o třech neznámých: a
a  =>
=>  =>
=> 
Dosadím do zadané rovnice:

Jak mám pokračovat dál? Předem děkuji za každou radu.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
- (téma jako vyřešené označil(a) Aquabellla)
#2 02. 06. 2012 23:21 — Editoval Tomas.P (02. 06. 2012 23:40) Příspěvek uživatele Tomas.P byl skryt uživatelem Tomas.P. Důvod: Špatné řešení.
#3 03. 06. 2012 00:35 — Editoval OiBobik (03. 06. 2012 08:57)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Extrémy implicitní funkce
↑ Aquabellla:
Ahoj,
myslím, že ↑ Tomas.P: má ve výpočtech či v úvaze nějakou chybu (těžko říct, když píše jen řetězce znaků bez komentáře), tak reaguji (a omlouvám se předem, jestli se nějak pletu):
Do zadané rovnice jsi dosadila za  , stejně tak ovšem můžeš dosadit za
, stejně tak ovšem můžeš dosadit za  (hledáš "body podezřelé z extrémů", což v případě hladkých fcí znamená stacionární body. Tedy v kterémkoli bodě, ve kterém by implicitně zadaná funkce nabývala extrém, jsou splněny rovnice
(hledáš "body podezřelé z extrémů", což v případě hladkých fcí znamená stacionární body. Tedy v kterémkoli bodě, ve kterém by implicitně zadaná funkce nabývala extrém, jsou splněny rovnice 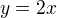 ,
,  . Jelikož ale bod
. Jelikož ale bod ![kopírovat do textarea $[x,y,z]$](/mathtex/92/923d8d0a14839c7de55c677ccbe0e875.gif) je bodem grafu implicitně zadané funkce, musí tento bod splňovat zadanou rovnici. Máme tedy zkrátka soustavu 3 rovnic o 3 neznámých, kterou řešíš). Dostaneš tak kvadratickou rovnici pro
je bodem grafu implicitně zadané funkce, musí tento bod splňovat zadanou rovnici. Máme tedy zkrátka soustavu 3 rovnic o 3 neznámých, kterou řešíš). Dostaneš tak kvadratickou rovnici pro  , její řešení (a zpětné dosazení pro výpočet y,z) ti dá jediné body "podezřelé z extrémů".
, její řešení (a zpětné dosazení pro výpočet y,z) ti dá jediné body "podezřelé z extrémů".
Dále lze postupovat standardně: v podezřelých bodech spočítat hessovu matici, určit, je-li poz-def/neg-def, atd.
Nebo:
Celý příklad lze taky řešit úplně naruby: a sice, že hledáme lokální extrémy funkce  vzhledem k množině
vzhledem k množině ![kopírovat do textarea $M=\{[x,y,z] \Big| x^2 + y^2 + z^2 - xy - \sqrt{2}yz - 1 = 0\}$](/mathtex/c7/c7a92abf46104b633ebeebfed830cc14.gif) .
.
Pak lze celý příklad řešit standardně Lagrangeovými multiplikátory.
(Tato dvě zadání teda nejsou zcela ekvivalentní, ale (myslím, že ) jde ukázat, že globální i lokální extrémy si budou odpovídat. Navíc tato druhá verze dává svým způsobem lepší smysl - neexistuje totiž žádná globální funkce f(x,y) daná implicitně onou rovnicí ze zadání, věta o implicitní funkci nám dává jen existenci lokálních funkcí na okolích vhodných bodů - viz wolfram - je jasné, že takový elipsoid není funkce proměnných x,y - i když "horní poloelipsoid" a "dolní poloelipsoid" jsou)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#4 03. 06. 2012 12:46
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Extrémy implicitní funkce
↑ Tomas.P:
Díky moc, jen si neumím představit, jak bych tento příklad počítala bez kalkulačky :-)
↑ OiBobik:
Tomášův postup mi smysl dává a přepočítávala jsem to a numerická chyba tam není. Každopádně jsem to zkoušela počítat i tím, cos psal ty, a vyšlo mi:  , takže v jednom z postupů chybka je.
, takže v jednom z postupů chybka je.
Každopádně děkuji oběma za rady, ty postupy se mi budou hodit :-)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#5 03. 06. 2012 13:30 — Editoval OiBobik (03. 06. 2012 13:45)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Extrémy implicitní funkce
↑ Aquabellla:
Pořád si myslím, že Tomášův postup je špatně...
Zdá se mi totiž, že v jeho postupu z nějakého důvodu začíná hledat "lokální extrémy implicitně zadané funkce  ", které ovšem nemusí mít s lokálními extrémy původní implicitně zadané funkce nic společného ("na co je potřeba mít lokálně maximalizováno y v bodě, kde chceme mít lokálně maximalizováno z?").
", které ovšem nemusí mít s lokálními extrémy původní implicitně zadané funkce nic společného ("na co je potřeba mít lokálně maximalizováno y v bodě, kde chceme mít lokálně maximalizováno z?").
Nevím, jak to lépe zdůvodňovat, řekl bych, že slovní popis výše (↑ OiBobik:) potvrzuje správnost mého postupu.
Možná snad ještě přidám následující wolframy:
globální maximum fce z na množině {x^2+y^2+z^2-xy-sqrt(2)y*z-1=0}
globální maximum fce y na množině {11/2 *x^2+y^2-4xy-1=0}
(píšu "globální extrémy" a ne lokální jen proto, aby tam ten wolfram neházel nějaké desetinné rozvoje - pravděpodobně řeší wolfram globální extrémy analyticky a lokální numericky; pro lokální extrémy dává wolfram stejné výsledky)
(Pozn: Nechcu tu do někoho rýpat nebo tak, jen si myslím, že by tu neměly být chybně řešené topicy)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#6 03. 06. 2012 13:52
Re: Extrémy implicitní funkce
↑ OiBobik:
Zdravím, svůj postup jsem opíral o zadání: určete lokální extrémy funkce  , tzn. fce dvou proměnných.
, tzn. fce dvou proměnných.
Offline
#7 03. 06. 2012 14:15 — Editoval OiBobik (03. 06. 2012 14:21)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Extrémy implicitní funkce
↑ Tomas.P:
Ahoj,
nezlob se, ale stále si myslím, že Tvůj postup je chybný.
Dobrým argumentem je snad toto:
Dle věty o implicitní funkci je fce  třídy
třídy  (tj. derivace všech řádů jsou spojité).
(tj. derivace všech řádů jsou spojité).
Tedy body lokálního maxima, minima musí nutně být stacionárními body funkce  - speciálně, je-li
- speciálně, je-li ![kopírovat do textarea $[x_0,y_0]$](/mathtex/88/886cc999fd9d89ef14ee01db805cbe10.gif) bod, v němž má funkce
bod, v němž má funkce  lokální maximum, pak nutně
lokální maximum, pak nutně  .
.
↑ Aquabellla: v úvodu správně spočítala, že 
Hodnota  v bodě
v bodě 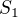 je (dosazením do původní rovnice) buď
je (dosazením do původní rovnice) buď  , nebo
, nebo  (viz odkaz)
(viz odkaz)
Dosazením Tebou vypočítaného bodu, v němž je nabyto lokálního maxima, pak v obou případech dostáváme
(kde jmenovatel má jistě smysl, jelikož  pro žádné z obou přípustných hodnot
pro žádné z obou přípustných hodnot  ).
).
Tedy funkce  nemůže mít v bodě
nemůže mít v bodě ![kopírovat do textarea $\[\frac{4}{11}\cdot \sqrt{\frac{11}{3}},\sqrt{\frac{11}{3}}\]$](/mathtex/a6/a612aa6d95d4ccfde2dc714370575412.gif) lokální extrém.
lokální extrém.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Extrémy implicitní funkce (TOTO TÉMA JE VYŘEŠENÉ)