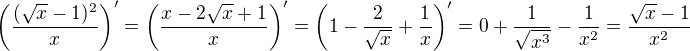Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 06. 2012 16:59 — Editoval Amaroun (03. 06. 2012 17:05)
První derivace
Dobrý den
Mám problém vypočítat dva příklady ohledně derivací
1)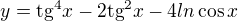
Dostal jsem po derivaci k takovémuto tvaru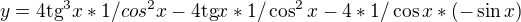
Bohužel nevím jestli je to není dobře anebo potom neumím náležitě upravit tvar do takto proklamovaného výsledku: 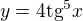
2)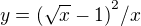
Tady tento příklad je asi velice jednoduchý, ale nemůžu přijít na správnou metodu, která by měla vésti k výsledku: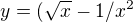
Děkuji za jakékoliv rady
Offline
- (téma jako vyřešené označil(a) jelena)
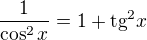 .
.