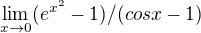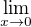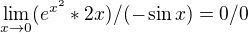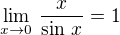Matematické Fórum

Amaroun

Dobrý den
Mám takovou to funkci:
$\lim_{x\to0}(e^{x^{2}}-1)/(cos x -1)$
Bohužel jsem se zasekl v nekonečné smyčce výpočtu, kdy se výsledek kvůli Eulerovu číslu vždy rozroste
Výsledek: -2
Je zde nějaký fígl?

Edit

jelena · 04. 06. 2012 10:15

Zdravím,

zkontroluj, prosím, zadaní. Pokud x->3, nejsou ani splněny podmínky pro použití l´Hospital (a lze jen dosazovat), ovšem pochybuji, že výsledkem bude -2.

Děkuji.

Amaroun · 04. 06. 2012 10:26

Ach jo.. Pardon to mne mrzí, má tam být $\lim_{x\to0}$

Rumburak · 04. 06. 2012 10:31

↑ Amaroun:

Zdravím.

Soudím, že má jít o 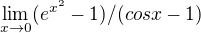$\lim_{x\to 0}(e^{x^{2}}-1)/(cos x -1)$ . Její výpočet 'lHosp. pravidlem by neměl být obtížný,
když využiješ znalost limity 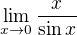$\lim_{x\to 0} \frac {x}{\sin x}$ .

Svůj problematický výpočet sem kdyžtak pošli, ať můžeme najít případnou chybu.

Amaroun

1) $\lim_{x\to0}(e^{x^{2}}-1)/(cos x -1)=0/0$
tedy derivace
2) $\lim_{x\to0}(e^{x^{2}}*2x)/(-\sin x)=0/0$
Opět neurčitý výraz
3) $\lim_{x\to0}(e^{x^{2}}*2x*2x+e^{x^{2}}*2x)*2/(-\cos x)=0/0$
A tady jsem po analyzování situace zjistil že ty členy by se jen rozšiřovali a výsledek by vyšel 0/0.

Cheop · 04. 06. 2012 10:59 — Editoval Cheop (04. 06. 2012 11:08)

↑ Amaroun:
Platí toto:
$\lim_{x\rightarrow 0}\,\frac{x}{\sin\,x}=1$
Takže:
$\lim_{x\rightarrow 0}\,\frac{e^{^{x^2}}-1}{\cos\,x-1}=\lim_{x\rightarrow 0}\,\frac{2x\cdot e^{^{x^2}}}{-\sin\,x}=\lim_{x\rightarrow 0}\,e^{^{x^2}}\cdot\lim_{x\rightarrow 0}\,\frac{2x}{-\sin\,x}=e^{0}\cdot (-2)=1\cdot(-2)=-2$

Amaroun · 04. 06. 2012 11:04

Děkuji pak je vše velice jednoduché.

Rumburak

↑ Amaroun:

A jestli můžu poradit, tak zápisy tvaru

(1) $\lim_{x\to0}(e^{x^{2}}-1)/(cos x -1)=0/0$

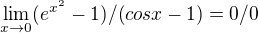
nepoužívej. Pokud někdy říkáme, že některá limilta je typu 0/0 , pak toto rčení i sám znak 0/0 je zálešitostí tzv. metajazyka,
jímž o matematichých pojmech a větách volně hovoříme (podobně jako třeba když říkáme "důkaz je obtížný", "tvrzení je triviální",
"definice je nepřehledná " atd.) , ale 0/0 rozhodně není matematický objekt, jemuž by mohla být rovna nějaká limita nebo který
by obecněji mohl být výsledkem matematického výpočtu.

Cynyc · 04. 06. 2012 11:43

↑ Amaroun: Znalost limity 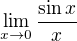$\lim_{x\to 0}\frac{\sin x}{x}$ zde není nutná. Vždy zkoušejte, za které členy lze dosadit. V tomto případě lze po L'Hospitalovi dosadit za 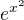$e^{x^2}$ a znovu L'Hospitalovat.

Amaroun

↑ Rumburak:
Dobrá... zapamatuji si to

↑ Cynyc:
Pochopil jsem správně, že tedy nemusím dosazovat do všech ale jen do 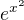$e^{x^{2}}$ , zatímco 2x nechám tak jak je? Stejně tak fuknci v jmenovateli? Nikdy jsem tento postup neviděl.

Honzc · 04. 06. 2012 12:17 — Editoval Honzc (04. 06. 2012 12:22)

↑ Amaroun:
Kdybys udělal tuto drivaci
$\lim_{x\to0}(e^{x^{2}}*2x)/(-\sin x)=0/0$
dobře
$\lim_{x\to0}2(e^{x^{2}}+e^{x^{2}}*2x*x)/(-\cos x)$
tak by ti vyšlo
$=2(1+0)/(-1)=\frac{2}{-1}=-2$

Cynyc · 04. 06. 2012 13:30 — Editoval Cynyc (04. 06. 2012 13:31)

↑ Amaroun: Pravidlo zní přesně tak, že pokud lze celou limitu rozdělit na součin nebo podíl dvou členů, z nichž (alespoň) jeden má konečnou nenulovou limitu, lze ho nahradit hodnotou této limity. Neboli v 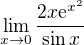$\lim_{x\to 0} \frac{2x\mathrm{e}^{x^2}}{\sin x}$ lze nahradit 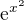$\mathrm{e}^{x^2}$ , které má limitu 1, ale ne $x$ a $\sin x$ , protože mají limitu nulovou. 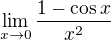V $\lim_{x\to 0} \frac{1-\cos x}{x^2}$ nelze nahradit nic, protože 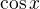$\cos x$ má sice limitu jedna, ale limitu nelze rozdělit na součin, kde by tento člen byl jením ze součinitelů. Podobné (ale méně užívané) pravidlo platí pro součet a rozdíl, kde stačí, aby limita nahrazovaného členu byla konečná. Obě pravidla jsou důsledkem tzv. druhé věty o aritmetice limit.