Matematické Fórum

Pavel · 07. 11. 2008 17:47 — Editoval Pavel (07. 11. 2008 17:59)

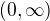Nech? funkce $f(x)$ je definovaná na intervalu $(0,\infty)$ , je na tomto intervalu omezená, diferencovatelná a existuje vlastní limita

$\lim_{x\to\infty}f'(x).$

Vyplývá odsud existence limity (a? už vlastní nebo nevlastní)

$\lim_{x\to\infty}f(x)?$

Tomsus · 07. 11. 2008 17:56

pokud se bere za limitu i +oo, tak bych si troufal tvrdit, ze ano

Pavel · 07. 11. 2008 17:59

↑ Tomsus:

Tak to dokaž :-)

Tomsus · 07. 11. 2008 18:10

ok - funkce je diferencovatelna, tudiz i spojita (ne, ze by mi to nejak pomohlo, ale je hezke si uvedomit, ze Riemann se tentokrat nekona :-)

necht ma f'(x) limitu ruznou od nuly - potom existuje bod a blablabla... proste se od nejakeho bodu na ose x bude pohybovat pouze v okolicku limity - tj bude ta derivace az do nekonecna pouze kladna, ci pouze zaporna --> f(x) bude tedy ryze rostouci anebo ryze klesajici - tj. bude mit limitu. (budto konecnou anebo nektere nekonecno)

no, a necht je tedy limita derivace nula..... tak to domyslim, protoze tam se muze pohybovat pod i nad nulou, tj. puvodni fce muze rust i klesat, ale zalezi na tom nakolik - asi to bude konvergovat k realne hodnote, ale to je zatim jen domenka

Tomsus · 07. 11. 2008 18:37

ok, tak vyuziju to, ze f' ma za primitivni fci f

ted by to vazne chtelo umet TeX :-)

to, ze existuje nulova limita znamena, ze od jisteho x a pro vsechna epsilon |f'(x)|<epsilon
toto plati i pro jejich primitivni fce - tj. |f(x)|<epsilon*x + C
jelikoz toto plati pro vsechna epsilo, blizi se |f(x)| k nejake konstante...

Q.E.D

Pavel · 07. 11. 2008 19:07 — Editoval Pavel (07. 11. 2008 19:07)

↑ Tomsus:

Problém vidím v tomto:

|f(x)|<epsilon*x + C

Ty zvolíš jakékoliv epsilon, jenže já Ti s x-em uteču hodně daleko k nekonečnu, takže epsilon*x nepůjde k nule :-) Pro velmi malé fixní epsilon, mohu najít hodně velké x, takže se ke konstantě s |f(x)| blížit nebudu :-)

Tomsus · 07. 11. 2008 19:11 — Editoval Tomsus (07. 11. 2008 19:19)

Stejne by to nefungovalo, protoze bych mel, ze |f(x)|<C, coz jeste neznamena, ze to neosciluje

ach jo, proste je "jasny", ze tam musi byt ta f(x) konstantni, kdyz se derivace blizi nule... ted me ale spis trapi teoreticka fyzika, takze s timhle asi ted na chvili koncim :-)

Pavel Brožek

Je vidět, že se nemůžeme spolehnout na intuici:

Inspirací pro mě byla funkce

$f'(x)=\frac12$ pro $x\in(0,\,1]$
$f'(x)=(-1)^n\cdot\frac{1}{2^n}$ pro $x\in(2^{n-1},\,2^n],\,n\in\mathbb{N}$

jejíž primitivní funkce nemá limitu v nekonečnu. Je ale moc hranatá, takže ji zpětně nemůžeme všude pěkně zderivovat. Když jsem ji ale viděl, tak mě hned napadla hezčí funkce

$f(x)=\sin(\ln(x))$