Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#4 05. 06. 2012 16:00 — Editoval Cynyc (05. 06. 2012 16:02)
Re: Limita posloupnosti
↑ Sulfan: Stirlingův vzorec je trochu kanón na vrabce a nevím, jestli ho máte dokázán, resp. jestli ho můžete používat bez důkazu (my jsme nemohli). Nejjednodušší, co mě napadá, je hrubý odhad faktoriálu zespoda 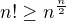 , který dostaneš tak, že spáruješ součinitele faktoriálu zvenku:
, který dostaneš tak, že spáruješ součinitele faktoriálu zvenku: 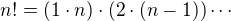 a každý z těchto součinů je větší nebo roven n. Je třeba to ještě trochu upřesnit (konkrétně že to platí pro sudá i lichá n), ale to už zvládneš. Lepší odhady se dají dostat pomocí integrálů, ale berete-li limity posloupností, zřejmě je ještě nemáte k dispozici.
a každý z těchto součinů je větší nebo roven n. Je třeba to ještě trochu upřesnit (konkrétně že to platí pro sudá i lichá n), ale to už zvládneš. Lepší odhady se dají dostat pomocí integrálů, ale berete-li limity posloupností, zřejmě je ještě nemáte k dispozici.
Offline
#5 05. 06. 2012 16:08 — Editoval Sulfan (05. 06. 2012 16:09)
Re: Limita posloupnosti
↑ Cynyc: Stirlingův vzorec zakázán nemáme, nicméně díky za Tvůj příspěvek, rozumím tomu postupu. Jinak integrály už máme probrané, toto je jen dílčí limita co slouží jako důkaz divergence jedné nekonečné řady. Jak by se to dalo odhadnout pomocí integrálu?
Offline
#6 05. 06. 2012 16:20 — Editoval Cynyc (05. 06. 2012 16:31)
Re: Limita posloupnosti
↑ Sulfan: Vyjde se z toho, že logaritmus udělá ze součinu součet, a ten se pak omezí integrálem shora i zdola: 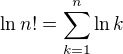 a
a 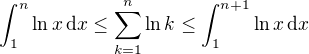 (není-li to jasné, nakresli si graf ln x a do něj ln k jako obdélníky o šířce 1 a výšce ln k, jednou vlevo od k a jednou vpravo). Když spočteš ty integrály a dáš jejich výsledek do exponentu e, dostaneš
(není-li to jasné, nakresli si graf ln x a do něj ln k jako obdélníky o šířce 1 a výšce ln k, jednou vlevo od k a jednou vpravo). Když spočteš ty integrály a dáš jejich výsledek do exponentu e, dostaneš 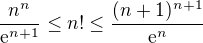 . Odnést by sis z toho měl podle mého hlavně tu myšlenku převodu faktoriálu na součet, to se hodí i jinde. Ale Stirlingův vzorec je samozřejmě ještě přesnější odhad, takže jste-li už tak daleko, je jeho použití nejsnažší. Já se akorát snažím učit studenty postupy, které jim dají lepší porozumění tomu, jak to vevnitř funguje, což použití vzorců, které nedokážou odvodit, není.
. Odnést by sis z toho měl podle mého hlavně tu myšlenku převodu faktoriálu na součet, to se hodí i jinde. Ale Stirlingův vzorec je samozřejmě ještě přesnější odhad, takže jste-li už tak daleko, je jeho použití nejsnažší. Já se akorát snažím učit studenty postupy, které jim dají lepší porozumění tomu, jak to vevnitř funguje, což použití vzorců, které nedokážou odvodit, není.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
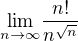 . Výsledek by měl být
. Výsledek by měl být  , ale nenapadá mě, jak se k němu dostat. Snažil jsem stanovit nějaký dolní odhad, ale to nezabralo.
, ale nenapadá mě, jak se k němu dostat. Snažil jsem stanovit nějaký dolní odhad, ale to nezabralo.