Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Riemannův integrál ze složené funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 11. 2008 09:39
Riemannův integrál ze složené funkce
Nech?  a
a  jsou Riemannovsky integrovatelné funkce na intervalu I. Vyplývá z tohoto předpokladu, že i funkce
jsou Riemannovsky integrovatelné funkce na intervalu I. Vyplývá z tohoto předpokladu, že i funkce 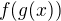 je na intervalu I Riemannovsky integrovatelná?
je na intervalu I Riemannovsky integrovatelná?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 07. 11. 2008 15:31 — Editoval Pavel (07. 11. 2008 15:45)
Re: Riemannův integrál ze složené funkce
↑ Tomsus:
Je otázka, zda podle Tvého zadání je 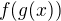 vůbec funkce. Abych se vyhnul těmto krajním případům, upřesním zadání:
vůbec funkce. Abych se vyhnul těmto krajním případům, upřesním zadání:
Nech?  a
a  jsou Riemannovsky integrovatelné funkce na intervalu I takové, že
jsou Riemannovsky integrovatelné funkce na intervalu I takové, že 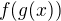 je funkce definovaná na intervalu I. Vyplývá z tohoto předpokladu, že i funkce
je funkce definovaná na intervalu I. Vyplývá z tohoto předpokladu, že i funkce 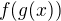 je na intervalu I Riemannovsky integrovatelná?
je na intervalu I Riemannovsky integrovatelná?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 07. 11. 2008 15:54
Re: Riemannův integrál ze složené funkce
↑ Tomsus:
Vzhledem k tomu, že Riemannova funkce je integrovatelná na každém intervalu I a g(x) je spojitá funkce zobrazující interval na interval, je f(g(x)) taky R-integrovatelná na I. Otázkou je, zda toto platí pro libovolnou dvojici funkcí f(x) a g(x) splňující výše uvedené podmínky.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 07. 11. 2008 16:06
Re: Riemannův integrál ze složené funkce
↑ Tomsus:
Je to tak, je třeba hledat protipříklad. Jen pro zajímavost, integrovatelnost Riemannovy funkce se probírala zde http://forum.matweb.cz/viewtopic.php?id=4465
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 07. 11. 2008 16:18
Re: Riemannův integrál ze složené funkce
↑ Tomsus:
Právě že znám jeden jednoduchý elegantní protipříklad :-) To byl důvod k tomu, abych založil toto téma. Jsi na správné stopě. Má to něco společného s Riemannovou funkcí.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#10 07. 11. 2008 16:37
Re: Riemannův integrál ze složené funkce
↑ Pavel:
Tak uz jsem konecne vymyslel funkci, kterou jsem chtel od zacatku. f(x)= sgn x, g(x)=Riemann(x)
tj. funkce f(g(x)) má vlastnosti na <0, +oo) - je rovna nule v iracionalnich bodech a 1 v racionalnich bodech - tj je to Dirichletova fce, ktera, jak vsichni dobre vime uz od skolky, Riemannovsky integrabilni neni
Offline
#12 07. 11. 2008 23:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Riemannův integrál ze složené funkce
Pavel napsal(a):
znám jeden jednoduchý elegantní protipříklad :-) To byl důvod k tomu, abych založil toto téma.
Toto sdělení (nebo sdělení podobného smyslu, účelu a obsahu) moc prosím umís?ovat do úvodního příspěvku tématu. Děkuji a zdravím :-)
--------------------
Pak zmizela někde na přídí, nepochybně aby vymyslela něco pekelně výchovného.
Offline
#13 08. 11. 2008 01:18
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Riemannův integrál ze složené funkce
↑ jelena:
Zdravím,
Proč? Já naopak prosím, aby tato informace v úvodním příspěvku nebyla, řešení je zajímavější, pokud dopředu nic nevíme a pak se můžeme zaradovat, když zjistíme jak to vlastně je :-)
Offline
#14 08. 11. 2008 11:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Riemannův integrál ze složené funkce
↑ BrozekP:
Zdravím :-)
to je ovšem psychologická otázka - já se raduji, když dopředu vím, že to dopadně dobře :-) :-) pak mi stačí jen ta radost a už níc neřeším :-)
Vážně - já jsem s Pavlem hovořila (mailem) - jelikož je už tady na fóru známo, že otázky formulované takovým způsobem nemám ráda, a to velmi. Nejde vůbec o obsah toho, sdělení, které jsem použila jako příklad (správně poznamenáváš, do VŠ nepatří), ale o způsob komunikace - plesk a dělejte.
Byla bych Pavlovi a ostatním autorům velmi vdečná, pokud začátek tématu měl úplně krátké sdělení pro ostatní, třeba "mám pro vás ...." "řešil jsem..." "rád bych se podělil...." - nemusí hlásit, že zná řešení.
Vzhledem ke kreativitě zajimavých úloh nepochybuji, že budete stejně kreativní také v úvodní větě (a? se mohu radovat :-)
Určitě to v tématu smažu, až se dohodneme (škoda sice citatů :-) Rozumime se ?
Děkuji moc :-)
--------------------
Potom za odměnu trochu výchovných her. Jsou tak prospěšné! A jakou dnes budeme mít výživnou, ale prostou strávu?"
"Kávu," pravil Kryšanek.
"Ne, kaši," opravila ho teta, "kavu pijeme, až když jsme staří a třeseme se."
Offline
#15 08. 11. 2008 11:22
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Riemannův integrál ze složené funkce
↑ jelena:
Myslím, že chápu, nešlo ti tedy o informaci, že Pavel má protipříklad (tak jsem to pochopil), ale o nějaký úvod k úloze.
Také nemám rád, když někdo přijde a pouze zkopíruje/opíše zadání nějaké úlohy (často ještě nesrozumitelně). Na zajímavé úlohy (zvláště od Pavla a Mariana) ale nahlížím jinak - nedávají je sem, aby jim to někdo vyřešil, ale dělí se s námi o zajímavé příklady, abychom si je také mohli vyřešit. U těchto úloh tedy úvod nepostrádám. Jestli však nějaký je, pak by podle mě neměl obsahovat žádnou informaci o řešení :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Riemannův integrál ze složené funkce (TOTO TÉMA JE VYŘEŠENÉ)