Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 05. 2012 22:11
Sdružená rozdělení ?
Uvažujme speciální střeleckou soutěž: Y značí počet pokusů, které má střelec v
jednom kole, přičemž předpokládejme, že Y je náhodné s binomickým rozdělením Bi(2; 1/2 ) (tj. střelec má v každém kole buď žádný, jeden nebo dva pokusy). Střelec má v každém pokusu úspěšnost 1/3 , tj. pokud vystřelí, pak s pravděpodobností 1/3 trefí terč. Označme X = 1, pokud střelec v daném kole trefil alespoň jednou terč, a X = 0, pokud střelec v daném kole netrefí terč ani jednou.
a) Určete sdružené rozdělení vektoru (X; Y ).
Nevíte, prosímvás, jak sestavit tabulku rozdělení vektoru ?
X/Y 0 1 2
0 1/4 1/3 1/9
1 0 1/6 5/36
takhle ta tabulka vypadá, ale jak se došlo k hodnotám ? Díky :)
Offline
#2 07. 06. 2012 08:37
Re: Sdružená rozdělení ?
Snad takto:
Použiju vzorec pro výpočet Binomického rozdělení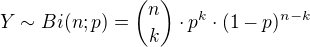
Vypočítám pravděpodobnost pro všechny k (0,1,2)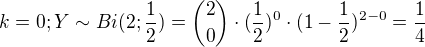
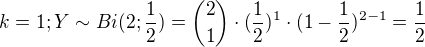
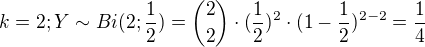
Teď provedu kombinaci pravděpodobností:
Když mám 0 pokusů, tak mám 100% šanci, že se nestrefím a 0% šanci, že se strefím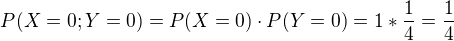
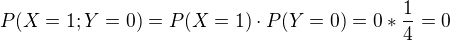
Když mám 1 výstřel, tak úspěšnost, dle zadání, je  a neúspěšnost logicky
a neúspěšnost logicky 
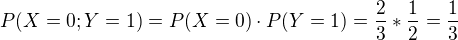
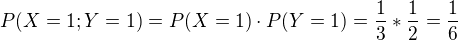
Když mám 2 výstřely, tak úspěšnost je stejná jako předchozí jen umocněná na 2.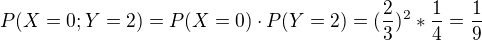
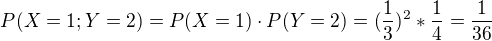
Poslední řádek z nějakého důvodu nevyšel, ale to nevadí, protože součet všech čísel musí být 1, takže součet všech přechozích se odečte od 1 a vyjde 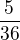
Offline
