Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 09. 11. 2008 10:39
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: limita
Rozšiř zlomek tak, aby limita jmenovatele bylo nenulové konečné číslo.
Offline
#5 09. 11. 2008 10:53 — Editoval BrozekP (09. 11. 2008 10:54)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: limita
↑ ttopi:
Ano, to je dobře. Já jsem chtěl navést k rozšíření 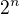 , což je to samé jako krácení
, což je to samé jako krácení 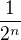 .
.
Edit: jen bych vynechal ta rovnítka uvnitř limit :-)
Offline
#6 09. 11. 2008 10:53
- apurvathea
- Příspěvky: 108
- Reputace: 0
Re: limita
↑ ttopi: asi to bude dobře, ve výsledkách mám -1. Děkuju
Offline
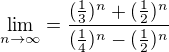
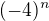 , ale to asi neexistuje...
, ale to asi neexistuje...