Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 06. 2012 23:02 — Editoval check_drummer (10. 06. 2012 20:11)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Vztah podgrup v grupě řádu q.p^n
Ahoj,
mějme grupu G řádu 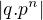 . Ta dle Sylowových vět obsahuje aspoň jednu podgrupu H řádu
. Ta dle Sylowových vět obsahuje aspoň jednu podgrupu H řádu 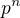 a aspoň jednu podgrupu F řádu
a aspoň jednu podgrupu F řádu  . Zajímalo by mě, zda je možné za nějakých předpokladů (či dokonce bez předpokladů) tvrdit, že [Edit]
. Zajímalo by mě, zda je možné za nějakých předpokladů (či dokonce bez předpokladů) tvrdit, že [Edit] 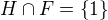 [\Edit]. Např. mě napadlo, že by tím předpokaldem mohlo být, že takových grup H existuje více (aspoň 2), případně přesně q, ale moc daleko jsem se nedostal.
[\Edit]. Např. mě napadlo, že by tím předpokaldem mohlo být, že takových grup H existuje více (aspoň 2), případně přesně q, ale moc daleko jsem se nedostal.
Rovněž by mě zajímalo, zda sjednocení všech takových H a F již tvoří G, nebo zda se může stát, že nějaké prvky "zbydou" - tj. nejsou obsaženy v žádné podgrupě řádu 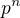 , nebo
, nebo  . Možná spolu obě otázky souvisí.
. Možná spolu obě otázky souvisí.
Díky za postřehy.
PS: Pokud téma nebude shledáno zajímavým, nejsem proti jeho přesunu do sekce "Vysoká škola".
"Máte úhel beta." "No to nemám."
Offline
#2 10. 06. 2012 12:26
Re: Vztah podgrup v grupě řádu q.p^n
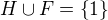 asi nenastane nikdy, ne?
asi nenastane nikdy, ne?
Pokud jsi chtěl napsat 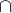 , tak to asi nastane vždy, pokud bude
, tak to asi nastane vždy, pokud bude 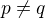 , prostě proto, že prvky v grupách mají různé řády.
, prostě proto, že prvky v grupách mají různé řády.
Offline
#3 10. 06. 2012 19:26 — Editoval OiBobik (11. 06. 2012 09:13)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Vztah podgrup v grupě řádu q.p^n
↑ check_drummer:
Ahoj,
co se týče druhé otázky (tj zda "všechny možné H,F pokryjí G"):
To obecně nebude pravda - stačí třeba uvážit grupu  . Pak
. Pak  , nebo i jakýkoli jiný generátor grupy, nemůže ležet v žádné netriviální podgrupě
, nebo i jakýkoli jiný generátor grupy, nemůže ležet v žádné netriviální podgrupě 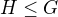 . (za předpokladu, že
. (za předpokladu, že  )
)
Dokonce to nebude platit v žádné komutativní grupě - je-li 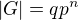 , pak (předpokládám-li, že
, pak (předpokládám-li, že  a
a  ), pak zvolím-li
), pak zvolím-li  a
a  , pak prvek
, pak prvek 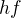 má řád, který nedělí ani
má řád, který nedělí ani  , ani
, ani 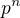 (v komutativní grupě je řád součinu dvou prvků nejmenší společný násobek řádů jednotlivých prvků, za těch předpokladů jsou tyto řády netriviální dělitelé
(v komutativní grupě je řád součinu dvou prvků nejmenší společný násobek řádů jednotlivých prvků, za těch předpokladů jsou tyto řády netriviální dělitelé  , resp.
, resp. 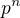 a jejich nejmenší násobek nedělí ani jedno z čísel, jelikož
a jejich nejmenší násobek nedělí ani jedno z čísel, jelikož 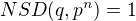 )
)
EDIT: "v komutativní grupě je řád součinu dvou prvků nejmenší společný násobek řádů jednotlivých prvků" - to je samozřejmě blbost. Ale pro prvky nesoudělných řádů určitě pořád platí, že řád součinu prvků je součin řádů prvků, takže ten protipříklad stále projde.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#4 10. 06. 2012 20:20
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Vztah podgrup v grupě řádu q.p^n
↑ Olin:
Ahoj, díky za upozornění, opravil jsem.
Spíš bych, řekl nejen, že mají různé, ale mají nesoudělné řády - proto by tento průnik (který sám je grupou) musel mít mohutnost, která dělí jak p^i, tak q, což jinak, než, že je tato mohutnost 1, nelze.
"Máte úhel beta." "No to nemám."
Offline
#5 10. 06. 2012 20:26
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Vztah podgrup v grupě řádu q.p^n
↑ OiBobik:
Jasně, díky. Asi jsem měl napsat, že mě zajímají výhradně grupy nekomutativní. Speciálně jsem na tuto otázku narazil při zkoumání důkazu, že každá grupa řádu q.p^n je řešitelná, což je zajímavé zkoumat jen pro případ, kdy je tato grupa nekomutativní. Bylo by zajímavé zjistit, zda v takových grupách už tvrzení o "pokrytí" platí.
"Máte úhel beta." "No to nemám."
Offline
#6 10. 06. 2012 20:36 — Editoval OiBobik (10. 06. 2012 20:54)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Vztah podgrup v grupě řádu q.p^n
↑ check_drummer:
Ok, tak přidám ještě jeden (umělejší, ale přece : D ) nekomutativní protipříklad:
Uvažme grupu 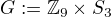 . Pak
. Pak 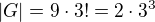 a prvek
a prvek 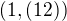 je řádu 18, tedy opět nemůže ležet v požadovaných podgrupách.
je řádu 18, tedy opět nemůže ležet v požadovaných podgrupách.
(Možná by to šlo s nějakým požadavkem na trivialitu centra grupy.)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#7 10. 06. 2012 22:31
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Vztah podgrup v grupě řádu q.p^n
↑ OiBobik:
Když o tom tak přemýšlím, tak spolu oba body souvisí - pokud budou mít uvedené grupy "typu" H dostatečně "malý" průnik a bude-li jich "dostatečně mnoho", pak na podgrupy(u) typu F zbydou všechny dosud "nepokryté" prvky - a zbyde-li jich málo, pak můžou tvořit (spolu s 1, který je pokryt každou grupou) celou grupu F. Ale bude to chtít nějaké dodatečné podmínky, jak ukazuje Tvůj příklad. (Pozn.: V důkaze řešitelnosti té grupy se operuje s normalizátorem grupy H.)
"Máte úhel beta." "No to nemám."
Offline