Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Riesz-Fischerova věta (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 06. 2012 17:23
Riesz-Fischerova věta
Ahoj,
mám trochu problém s kombinací Besselovy nerovnosti a Riesz-Fischerovy věty.
Na přednášce jsme si zapsali Besselovu nerovnost
Nech't 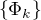 ,
, 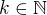 je ortonormální systém v
je ortonormální systém v  Hilbertově prostoru,
Hilbertově prostoru,  . Potom
. Potom  a též \sum c_k^2 \le ||f||_H^2.
a též \sum c_k^2 \le ||f||_H^2.
Pak máme Riesz-Fischerovu větu, která již ve znění předpokládá  . Když toto platí pak
. Když toto platí pak 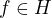 tak, že
tak, že 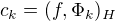 a
a 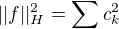 .
.
Přítomnos nerovnosti si v Besselově nerovnosti vysvětlují tím, že systém 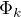 nemusí být úplný. Ale když dokazujeme Riesz-Fischerovu větu vlstně nevyužijeme žádných dalších předpokladů oproti větě ukazující Besselovu nerovnost. Jak je tedy možné,
nemusí být úplný. Ale když dokazujeme Riesz-Fischerovu větu vlstně nevyužijeme žádných dalších předpokladů oproti větě ukazující Besselovu nerovnost. Jak je tedy možné,
že tam striktně platí rovnost?
Díky moc za odpověď.
pi = 3
Offline
- (téma jako vyřešené označil(a) jelena)
#2 12. 06. 2012 17:56 — Editoval OiBobik (12. 06. 2012 18:14)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Riesz-Fischerova věta
↑ Azeret:
Ahoj,
řekl bych, že jde zhruba o toto:
Příklad:
Uvaž 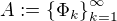 že je úplný ortonormální systém.
že je úplný ortonormální systém.
Pak 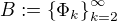 je taky nějaký ortonormální systém (který není maximální, tedy ani úplný).
je taky nějaký ortonormální systém (který není maximální, tedy ani úplný).
Buď 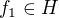 , kde
, kde  je náš Hilbertův prostor,
je náš Hilbertův prostor, 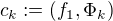 .
.
Z úplnosti systému  a z úplnosti prostoru plyne, že
a z úplnosti prostoru plyne, že 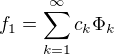
Speciálně (zobecněná Pythagrova věta) 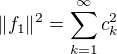
Platí tedy: 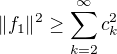 ... což je to, o čem mluví Besselova nerovnost (použitá na
... což je to, o čem mluví Besselova nerovnost (použitá na 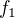 a ON systém
a ON systém  ).
).
Položme 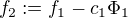 . Pak zřejmě
. Pak zřejmě  a platí
a platí 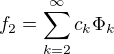 , speciálně
, speciálně 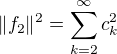 ... to je ta funkce, jejíž existenci deklaruje Riesz-Fisher (použitá na
... to je ta funkce, jejíž existenci deklaruje Riesz-Fisher (použitá na 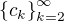 a systém
a systém  ).
).
___________________________________________________________________________________________
Příklad měl demonstrovat to, že: To, že pro nějakou fci s Four. koeficienty 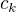 vzhledem k ON systému
vzhledem k ON systému  nenastává rovnost v Besselově nerovnosti, neznamená, že neexistuje funkce se stejnými Four koeficienty
nenastává rovnost v Besselově nerovnosti, neznamená, že neexistuje funkce se stejnými Four koeficienty 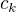 vzhledem k ON systému
vzhledem k ON systému  taková, že nastává přímo rovnost.
taková, že nastává přímo rovnost.
Snad to nebylo moc zmatečné, pointa je: Besselova nerovnost se vyjadřuje o konkrétní funkci, kterou dostanu. Riesz-Fisher hledá funkci na základě předepsaných skalárních součinů. Lze si to představit tak, že neúplný ON systém je (Schauderovou) bází nějakého uzavřeného podprostoru. Když bude  spadat do toho podprostoru, pak nastává rovnost v Besselově nerovnosti. Když ne, pak existuje alespoň "ortogonální projekce" fce
spadat do toho podprostoru, pak nastává rovnost v Besselově nerovnosti. Když ne, pak existuje alespoň "ortogonální projekce" fce  na ten podprostor.
na ten podprostor.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 12. 06. 2012 18:17
Re: Riesz-Fischerova věta
↑ OiBobik:
Díky moc! Teď je mi to úplně jasné! Paráda, proč takovýhle příklad nemáme v knížce . . .
pi = 3
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Riesz-Fischerova věta (TOTO TÉMA JE VYŘEŠENÉ)