Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 06. 2012 21:47
Kombinace
Zdravím,
prosím o pomoc s tímto příkladem:
Kolika způsoby lze 4dívky a 8chlapců rozdělit na dvě šestičlenná družstva tak, aby každém družstvu byla dvě děvčata a čtyři chlapci??
Ať se snažím, jak se snažím..stále nedostávám správný výsledek:420.
Prosím o radu, jak na to.
Děkuji.
Offline
#4 11. 06. 2012 22:10
Re: Kombinace
↑ machkat:
Jen bych doplnil, že takto to funguje, když jsou ta družstva nějak ozančená - třeba Sparta a Slávie.
Pokud ta družstva nejsou označená a rozpoznáváme je jen podle lidí, kteří v družstvu jsou, tak se to celé musí vydělit dvěma.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 12. 06. 2012 17:27
Re: Kombinace
↑ zdenek1:
Ahoj,
chtěla bych velmi poprosit o dodatečné vysvětlení, proč se musí výsledek ne/dělit dvěma v případě ne/označených skupin?
Je to z toho důvodu, že už byli jednou započítáni do první skupiny a tudíž by se objevili ve způsobech uspořádání 2x stejně? Šlo by to prosím ukázat na zadání nějakého konkrétního příkladu?
Velmi děkuji, K.
Offline
#6 12. 06. 2012 18:00
Re: Kombinace
↑ KDPK:
Přesně tak.
K tomu už těžko něco dodat.
představ si že máš holky A, B, C, D
a v nějaké výběru vybereš A a B. Zůstali ti C a D v druhém družstvu.
ale protože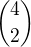 
jsou všechny výběry, tak někdy jindy
vybereš C a D zase spolu a zůstanou ti do druhého družstav A a B.
A když družstva rozlišuješ jen podle lidí, tak to nerozeznáš.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline