Matematické Fórum

Cynyc · 13. 06. 2012 22:44 — Editoval Cynyc (13. 06. 2012 22:46)

Ahoj,

jak nejjednodušeji dokázat, že $\mathrm{e}^x$ nelze vyjádřit z konstant a mocninných a odmocninných funkcí pomocí konečného počtu aritmetických operací a skládání?

OiBobik

↑ Cynyc:

Ahoj,

napadá mě celkem divoký argument, tak mě kdyžtak, prosím, někdo zastavte, kdybych mlel naprosté nesmysly : ))

Pro jednoduchost budeme funkci, která je konečným složením fcí
-identita
-přičtení konstanty
-násobení konstantou
-sečtení funkcí
-vynásobení funkcí
-mocnění na nějaký konstantní (kladný reálný, nebo racionální) exponent
říkat "dobrá funkce".

Pak pro každnou dobrou funkci $f(x)$ takovou, že je definovaná na nějakém okolí $+\infty$ , platí: $\exists r \geq 0: \lim_{x \to \infty}\frac{f(x)}{x^r}=0$

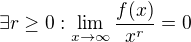
Důkaz tohoto by snad měl projít indukcí podle složitosti funkce $f$ (zítra se k tomu ještě vrátím).

No a teď:

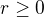Buď $f(x)$ libovolná dobrá funkce, která je definovaná alespoň na nějakém okolí $\infty$ (jiné zřejmě uvažovat není třeba). Nechť je $r\geq 0$ příslušný exponent. Pak
$\lim_{x \to \infty}\frac{f(x)}{e^x}=\lim_{x \to \infty}\frac{f(x)}{x^r}\cdot \frac{x^r}{e^x}=^{(VAL)}0 \cdot 0=0$ .

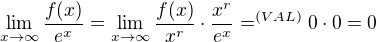Tedy speciálně 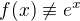$f(x) \not \equiv e^x$ na nějakém okolí $\infty$ ... jinak by limita v nekonečnu nutně musela vycházet $1$ (jelikož by platilo $\frac{f(x)}{e^x}\equiv 1$ ).

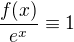Neboli, stručněji: exponenciela roste v nekonečnu příliš rychle na to, aby to byla dobrá funkce.

Cynyc · 13. 06. 2012 23:43 — Editoval Cynyc (14. 06. 2012 01:03)

↑ OiBobik: Tohle me napadlo také, jenže to funguje jen pokud z aritmetických operací vyřadíme dělení, resp. pokud vyřadíme mocninné funkce se záporným exponentem.

Matematické Fórum

#1 13. 06. 2012 22:44 — Editoval Cynyc (13. 06. 2012 22:46)

(Ne)vyjádřitelnost exponenciely pomocí mocnin a odmocnin

#2 13. 06. 2012 23:36 — Editoval OiBobik (13. 06. 2012 23:49)

Re: (Ne)vyjádřitelnost exponenciely pomocí mocnin a odmocnin

#3 13. 06. 2012 23:43 — Editoval Cynyc (14. 06. 2012 01:03)

Re: (Ne)vyjádřitelnost exponenciely pomocí mocnin a odmocnin

Zápatí