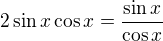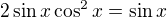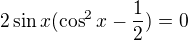Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 06. 2012 10:57
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Goniometrické vzorce
Mám rovnici 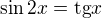 tu si podle vzorce rozložím na
tu si podle vzorce rozložím na 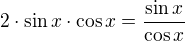 dále jsem vynásobila cosx, pak různě pokrátila a došlak rovnici
dále jsem vynásobila cosx, pak různě pokrátila a došlak rovnici 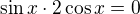 ale z toho mi nevychází řešení rovnice
ale z toho mi nevychází řešení rovnice 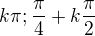 . Poradíte mi prosím kde mám chybu?
. Poradíte mi prosím kde mám chybu?
Offline
- (téma jako vyřešené označil(a) terezkaaaaa5)
#3 17. 06. 2012 11:09
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Goniometrické vzorce
↑ Sulfan:
Nechápu, jak se z toho předposledního výrazu stal ten poslední? Vysvětlíš mi to prosím? A kde na začátku dělíme 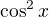 ?
?
Offline
#4 17. 06. 2012 11:17 — Editoval Sulfan (17. 06. 2012 11:17)
Re: Goniometrické vzorce
↑ terezkaaaaa5: To s tím dělením 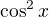 jsem přehlédl, samozřejmě určujeme jen existenci
jsem přehlédl, samozřejmě určujeme jen existenci 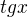 tj
tj 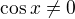 .
.
Podrobně rozepíšu poslední krok: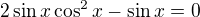
vytknu jen samotný  (to by mělo být jasné):
(to by mělo být jasné):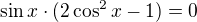
nyní vytknu ještě dvojku ze závorky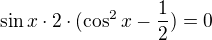
Což je součin dvou výrazů rovný nule, tudíž rozlišíme případy, kdy se jeden činitel rovná nule a kdy se rovná nule druhý.
Offline
#5 17. 06. 2012 11:22
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Goniometrické vzorce
↑ Sulfan:
Díky. Takže sin je roven nule vždy po periodě  . A cos x v tomto příkladě vychází
. A cos x v tomto příkladě vychází 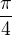 . Ale co ta perioda
. Ale co ta perioda 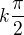 ?
?
Offline
#6 17. 06. 2012 11:30
Re: Goniometrické vzorce
↑ terezkaaaaa5: Tam není 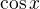 , ale
, ale 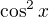 . Tj. řešíme rovnici
. Tj. řešíme rovnici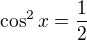
Teď ji odmocním, ale musíme dávat pozor, protože jak víme 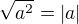 Tj absolutní hodnota.
Tj absolutní hodnota.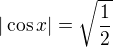
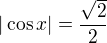
Zároveň platí, že rovnice ve tvaru 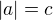 je ekvivalentní vyjádření
je ekvivalentní vyjádření 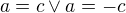 , v našem případě:
, v našem případě: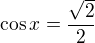 nebo
nebo 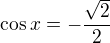
A to už vyřešíme snadno, první řešení rovnice je: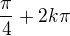
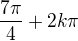
Druhé rovnice: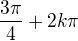
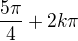
Sama můžeš oveřit, že se tak dostanou všechny liché násobky 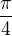
Offline