Matematické Fórum

ajeto · 20. 06. 2012 16:17

Dobrý deň

veta znie nasledovne:
Nech $y(x),z(x)$ sú netriviálne lineárne nezávislé riešenia rovnice
$y''+p(x)y'+q(x)y=0$ kde $p,q$ sú spojité funkcie.
Potom medzi ľubovoľnými dvomi susednými nulovými bodmi riešenia $z$ leží nulový bod riešenia $y$ a naopak.

Mám k nej nasledovný dôkaz

Nech $z(x_1)=0=z(x_2)$ a $z(x)\neq 0\,,\,\forall x \in (x_1,x_2)\,,\,x_1<x_2$ . $(1)$

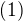
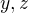$y,z$ sú lineárne nezávislé, potom pre wronskián platí

$W(y,z,x)=\left|\begin{array}{cc}y(x)&z(x)\\y'(x)&z'(x)\end{array}\right|=y(x)z'(x)-z(x)y'(x)\neq 0$ .

Z toho pre i=1,2 platí $W(y,z,x_i)=y(x_i)z'(x_i)\neq 0$

teda $y(x_i)\neq 0\wedge z'(x_i)\neq 0$ .

Z predpokladu 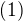$(1)$ vyplýva, že $z'(x_1)$ a $z'(x_2)$ nemajú rovnaké znamienka.

$\star$ Potom $\exists x_0 \in (x_1,x_2)\,:\,y(x_0)=0$ . $\star$

takto to mám zapísané,
ale nie je mi jasné odkiaľ máme tú implikáciu čo som zapísal medzi hviezdičky.

Vďaka za každú odpoveď

kaja.marik · 20. 06. 2012 16:42

y(x) taky na (x_1,x_2) meni znamenko. To proto, ze wronskian znamenko nemeni (Liouvilluv vzorec) a potom se pouzije veta toho pana

ajeto · 20. 06. 2012 17:13

↑ kaja.marik:

jasne, to s tým wronskiánom mi úplne uniklo :)

a hádam by som pre $y$ mohol použiť aj Darbouxovu vlastnosť pre spojitú funkciu potom

vďaka :)

kaja.marik

Asi ano. Ale treba tuhle darb. vlstnost znam jako druhou Bolzanovu vetu a Bolzano zil drive.

vanok · 20. 06. 2012 17:32 — Editoval vanok (20. 06. 2012 17:37)

Ahoj,
Ja by som skor to dokazal takto ( upravil som to na tvoje ozancenia)
Nech $y(x),z(x)$ sú netriviálne lineárne nezávislé riešenia rovnice
$y''+p(x)y'+q(x)y=0$ kde $p,q$ sú spojité funkcie.
Potom medzi ľubovoľnými dvomi susednými nulovými bodmi riešenia $z$ leží nulový bod riešenia $y$ a naopak.

Dôkaz

Nech $z(x_1)=0=z(x_2)$ a $z(x)\neq 0\,,\,\forall x \in (x_1,x_2)\,,\,x_1<x_2$ . $(1)$

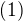
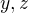$y,z$ sú lineárne nezávislé, potom pre wronskián platí

$W(y,z,x)=\left|\begin{array}{cc}y(x)&z(x)\\y'(x)&z'(x)\end{array}\right|=y(x)z'(x)-z(x)y'(x)\neq 0$ .

Z toho pre i=1,2 platí $W(y,z,x_i)=y(x_i)z'(x_i)\neq 0$

teda $y(x_i)\neq 0$ .kde $i \in \{1;2 \}$
[potialto to iste ako tvoj dokaz]
Teraz predpokladam ze $y(x) \neq 0,\forall x \in [x_1,x_2]\,,\,x_1<x_2$
To mi umoznuje dobre definovat funkciu $\frac z y$ na $[x_1,x_2]$
Mame
$\frac z y(x_1)=\frac z y(x_2)=0$
jej derivacia je nulova v nejakom bode $x_0 \in ]x_1,x_2[$
(Rolle-ova teorema)
Ale vdaka tomu, co sme dokazali $\frac {d } {dx} $ \frac z y $= \frac {-W(y,z,x)}{y(x)^2} \neq 0$
Tento spor zarucuje, ze existuje aspon jeden koren funkcie $y$ v $]x_1,x_2[$

Unicita: Ak by existovali dva korene na tomto intervale: $k_1; k_2$
tak symetricky by existoval aspon jeden $k_3$ funkcie $z$ medzi $k_1; k_2$ , co by protirecilo tomu, ze $x_1; x_2$ su dva nasledovne korene funkcie $z$

ajeto · 20. 06. 2012 18:06

↑ kaja.marik:

pravda, myslel som presne tú vlastnosť, takže hovoríme o tom istom :)

↑ vanok:

vďaka za ďalší jednoduchý spôsob ( $]a,b[$ je, predpokladám, značenie otvoreného intervalu?)

a za postreh ( samozrejme dôkaz tvrdenia je kompletný až s časťou o jednoznačnosti ktorú uvádzate na záver
svojho príspevku)

no, teplo dnes so mnou robí očividne svoje :)

vanok · 20. 06. 2012 18:14

↑ ajeto:
Ano to je tradicne znacenie vo Fr.

kaja.marik

Jeste na doplneni naznacim dalsi dve metody dukazu.

Da se zintegrovat Piconeho identita pro p_1=p_2 a q_1=q_2 od jednoho korene funkce u do druheho za predpokladu, ze v nema nulovy bod. Nalevo vyjde nula, napravo vyjde ze u'/u = v'/v a tedy v je nasobek u, coz je spor s nezavislosti. Tedy v nemuze byt kladna mezi dvema koreny funkce u. Je to vlastne specialni pripad srovnavaci vety.

Dalsi dukaz je zalozeny na substituci w=r*u'/u, ktera rovnici prevede na Riccatiho rovnici, coz je rovnice prvniho radu a daji se pouzit klasicke vety o diferencialnich nerovnostech. http://en.wikipedia.org/wiki/Riccati_eq … r_equation

Matematické Fórum

#1 20. 06. 2012 16:17

Otázka ku dôkazu vety o oddeliteľnosti nulových bodov

#2 20. 06. 2012 16:42

Re: Otázka ku dôkazu vety o oddeliteľnosti nulových bodov

#3 20. 06. 2012 17:13

Re: Otázka ku dôkazu vety o oddeliteľnosti nulových bodov

#4 20. 06. 2012 17:20 — Editoval kaja.marik (20. 06. 2012 17:21)

Re: Otázka ku dôkazu vety o oddeliteľnosti nulových bodov

#5 20. 06. 2012 17:32 — Editoval vanok (20. 06. 2012 17:37)

Re: Otázka ku dôkazu vety o oddeliteľnosti nulových bodov

#6 20. 06. 2012 18:06

Re: Otázka ku dôkazu vety o oddeliteľnosti nulových bodov

#7 20. 06. 2012 18:14

Re: Otázka ku dôkazu vety o oddeliteľnosti nulových bodov

#8 20. 06. 2012 18:57 — Editoval kaja.marik (20. 06. 2012 18:59)

Re: Otázka ku dôkazu vety o oddeliteľnosti nulových bodov

Zápatí