Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 06. 2012 15:09
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Priestor
↑ BakyX:
Ahoj, prostorem je myšlen E3? Předpokládám, že zadání je myšleno tak, že pro jakékoliv dvě přímky p,q, které jsou ve vybraném pokrytí, jsou p,q mimoběžné, že? Díky.
"Máte úhel beta." "No to nemám."
Offline
#3 23. 06. 2012 21:01
Re: Priestor
↑ check_drummer:
Dobrý deň.
Priestor myslím v stredoškolskom zmysle.
Pokrytie mimobežkami myslím pokrytie priamkami spĺňajúce:
a) Každý bod priestoru leží na práve jednej z týchto priamok.
b) Každé dve priamky sú mimobežné.
1^6 - 2^6 + 3^6 = 666
Offline
#4 24. 06. 2012 08:55
Re: Priestor
Můj laický pohled říká, že to nelze.
Představme si množinu mimoběžek, které mají společnou příčku. Dohromady tvoří takovou plochu, co vypadá trochu jako lodní šroub. Teď do toho lez napasovat další sadu mimoběžek se stejnou příčkou, která je kolmá na příčku první sady mimoběžek. Máme tedy dvě plochy v prostoru.
Teď, a to už si neumím pořádně představit, si myslím, že mezi tyto dvě sady mimoběžek by šla nacpat ještě třetí sada s příčkou opět kolmou na první a druhou příčku.
Tímto máme v prostoru tři plochy tvořené přímkami směřujícími do všech směrů. Teď už nelze sestrojit žádnou přímku, která by byla mimoběžkou k ostatním, protože každá nová přímka by musela být rovnoběžná s nějakou už ležící v jedné ze tří množin mimoběžek.
No a protože celý třírozměrný prostor nelze zcela zaplnit pouhýma třema plochama, nelze celý prostor zaplnit pouze mimoběžkama.
Bohužel toto vysvětlení silně zaostává za rigorozitou, tak nemám jistotu, že to tak opravdu je.
100*0>0 aneb stokrát nic umořilo osla
Offline
#5 24. 06. 2012 09:33
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Priestor

Na obrázku (z wikipedie) jsou přímky, které tvoří hyperboloidy. Zdá se mi (nic jsem se nesnažil dokázat), že přímky z různých hyperboloidů svírají různý úhel s vodorovnou rovinou, nemůžou být tedy rovnoběžné, a protože hyperboloidy vytvoří různé plochy, tak se ani nikde neprotínají. Když vezmeme dvě přímky z jednoho hyperboloidu, tak se taky nikde neprotnou a taky nejspíš nebudou rovnoběžné. A takovými různými hyperboloidy (+ svislá přímka) by podle mě mohlo jít prostor pokrýt. Teď jen takové přímky popsat matematicky a dokázat, že jsou skutečně všechny mimoběžné a pokrývají prostor.
Offline
#6 24. 06. 2012 10:36 — Editoval Pavel Brožek (24. 06. 2012 10:38)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Priestor
Svislá přímka procházející počátkem společně se všemi přímkami popsanými dvěma parametry  a
a 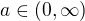 jejichž parametrické vyjádření je
jejichž parametrické vyjádření je
kde 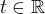 , podle mě tvoří pokrytí prostoru mimoběžkami.
, podle mě tvoří pokrytí prostoru mimoběžkami.
Offline
#7 24. 06. 2012 11:05 — Editoval OiBobik (24. 06. 2012 11:20)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Priestor
↑ Pavel Brožek:
Ahoj,
přesně to mě taky napadlo (nebo aspoň návodná představa byla podobná).
Tak to tady aspoň sepíšu, když už jsem si to rozmýšlel. (Jakmile člověk tuší, jaký systém hledat, je to už jen překvapivě jednoduchá lineární algebra.)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#8 24. 06. 2012 13:05
Re: Priestor
Ahoj ↑ OiBobik:,
Pekne riesenie.
A hned dalsie otazky:
1)ako popisat ine (alebo, dokonca vsetki) "rodiny" vyhovujucych priamok.
2) existuje aj synteticky dokaz tejto vlasnosti ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 24. 06. 2012 15:32 — Editoval vanok (24. 06. 2012 15:33)
Re: Priestor
Ahoj ↑ BakyX:,
Tvoj problem je z teto istej kategorie specialnych problemov (z pripravy na IMO 2009), aspon podla tohto pdf http://sas.uwaterloo.ca/~cgsmall/worksheet1.pdf
kde to je problem N°9.
A co si myslis o inych problemoch na tom pdf?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 24. 06. 2012 18:13 — Editoval OiBobik (24. 06. 2012 18:15)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Priestor
↑ vanok:
Ahoj,
1) No jedna přímočará myšlenka, jak nalézt další, je variace na tuto jednu: třeba uvažovat rodiny  . Dokonce bych řekl (to teda nemám dokázané, ale geometricky se zdá, že by to mohlo platit), že to budou splňovat i rodiny
. Dokonce bych řekl (to teda nemám dokázané, ale geometricky se zdá, že by to mohlo platit), že to budou splňovat i rodiny  , kde
, kde  je nějaká nerostoucí kladná (nebo naopak: neklesající záporná) spojitá funkce.
je nějaká nerostoucí kladná (nebo naopak: neklesající záporná) spojitá funkce.
Další zobeznění může být: použít na takové systémy M nějakou transformaci grupy  (tj. nějakou shodnost), které zřejmě zachovávají požadované vlastnosti.
(tj. nějakou shodnost), které zřejmě zachovávají požadované vlastnosti.
Ale to má do charakterizace všech řešení pravděpodobně hodně daleko (všechno to jsou v podstatě pořád ty hyperboloidy).
(ty znáš ještě nějaká řešení?)
2) Co je myšleno syntetickým důkazem? Důkaz, nevyužívající analytické geometrie?
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#11 24. 06. 2012 19:02 — Editoval vanok (24. 06. 2012 19:04)
Re: Priestor
ahoj ↑ OiBobik:,
Synteticka geometria je
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.
ako je to vyjadrene v http://en.wikipedia.org/wiki/Synthetic_geometry.
Tvoje riesenie, som interpretoval, ze si v affinom priestore,
kde mas dve roviny
Prva co prechadza pociatkom
druha, rovnobezna z prvou, prechadzajuca bodom (0; 0; 1).
Tvoje generacne mimobezky su vytvorene, tebou urcenymy bodmy tychto dvoch rovin.
A potom (x,y)-->(y, -x) je "rotacia "... uhla 
V niecom je to velmi sympaticka rodina, lebo napr. usecka v prvej rovine je tiez v druhej a potom sa mo zda ze aj v kazdej rovnobezbzj rovine z tymito.
Iste pre ine "rotacie" su ine "rodiny" priamok
Ale pre ine konstrukcie ( vdaka tvojich rovinaml) co som testoval, sa mi sa mi nepodarilo ukazat surjektivitu...
Inac v pdf, co som poslal kolegovy ↑ vanok: su tiez ine pozoruhodne problemy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 Vzhledem k třetím souřadnicím pak ovšem
Vzhledem k třetím souřadnicím pak ovšem 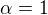 a
a 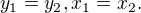 Tedy přímky
Tedy přímky 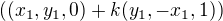 a
a 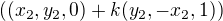 se shodují.
se shodují. . Porovnáním třetích složek opět dostáváme
. Porovnáním třetích složek opět dostáváme  . Pak (rozepsáním rovnice pro první dvě složky)
. Pak (rozepsáním rovnice pro první dvě složky)

 , pak
, pak 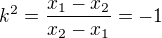 , spor.
, spor. pak y druhé rovnice vidíme, že
pak y druhé rovnice vidíme, že 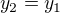 a přímky
a přímky  pokrývá
pokrývá 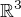 :
: bod z
bod z 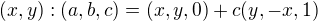
 ,
, . Matice je tedy regulární a řešení vždy existuje. Existuje tedy přímka ze systému
. Matice je tedy regulární a řešení vždy existuje. Existuje tedy přímka ze systému