Matematické Fórum

jarrro · 02. 07. 2012 16:56

ahoj na wikipedii píšu, že existuje funkcia, ktorá nie je žiadnej (ani nekonečnej) Baireovej triedy.
dá sa takáto funkcia nejako popísať? alebo je to len čisto existenčná záležitosť?
Baireovou triedou myslím, že nultá Baireova trieda sú spojité funkcie a k-ta Baireova trieda sú bodové limity funkcií z nižších Baireových tried, ale nepatriace do žiadnej nižšej Baireovej triedy.
Asi tá funkcia bude pekne škaredá, lebo napr. aj všade nespojitá Dirichletova funkcia patrí už do druhej Baireovej triedy.

Rumburak

↑ jarrro:
Ahoj.

Uvažujme funkce definované v $\mathbb{R}^n$ .

Platí věta, že každá baireovské funkce je měřitelná (ve smyslu Lebesgueovy teorie integrálu).

(Protože
- spojité funkce jsou měřitelné,
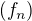- je-li funkce $f$ limitou (při bodové konvergenci) posloupnosti $(f_n)$ měřitelných funkcí, pak i $f$ je měřitelná. )

Vezmeme-li v $\mathbb{R}^n$ lebesgueovsky neměřitelnou množínu, pak její charakteristická funkce není měřitelná a tudíž ani baireovská.

jarrro · 02. 07. 2012 17:34

díky to by ma nenapadlo a ako jednoduché to je

jarrro · 03. 07. 2012 09:43

ešte ma napadlo existuje aj merateľná nebaireovská funkcia? alebo je baireovskoť ekvivalentná s merateľnosťou?

Rumburak · 03. 07. 2012 10:22

↑ jarrro:
Tak toto bohužel nevím ...

jarrro · 04. 07. 2012 10:34

tak googlil som a vyzerá to tak, že merateľná nebairovská funkcia existuje, ale od baireovskej s líši len na množine miery nula. dokonca každá merateľná funkcia je skoro baireovská s indexom menším najviac rovným 2.

Rumburak · 04. 07. 2012 10:53

↑ jarrro:
No to je velmi zajímavé, děkuji za informaci.
Já jsem mezitím zase našel toto.

jarrro · 04. 07. 2012 12:06

↑ Rumburak:díky zaujímavé, že v bežnom živote exotičnosti sú v matematike typické veci

Matematické Fórum

#1 02. 07. 2012 16:56

nebaireovská funkcia

#2 02. 07. 2012 17:19 — Editoval Rumburak (03. 07. 2012 11:05)

Re: nebaireovská funkcia

#3 02. 07. 2012 17:34

Re: nebaireovská funkcia

#4 03. 07. 2012 09:43

Re: nebaireovská funkcia

#5 03. 07. 2012 10:22

Re: nebaireovská funkcia

#6 04. 07. 2012 10:34

Re: nebaireovská funkcia

#7 04. 07. 2012 10:53

Re: nebaireovská funkcia

#8 04. 07. 2012 12:06

Re: nebaireovská funkcia

Zápatí