Matematické Fórum

FliegenderZirkus

Dobrý večer,

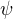mám materiálový model $\psi(\mathbf{C})=\mathrm{tr}\left(\ln\left(\sqrt{\mathbf{C}}\right)\right)$ , kde C je pravý Cauchy-Greenův tenzor a $\psi$ je deformační energie. Pro vyjádření druhého Piola-Kirchhoffova tenzoru napětí S je potřeba tuto funkci zderivovat: 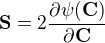$\mathbf{S}=2\frac{\partial \psi(\mathbf{C})}{\partial \mathbf{C}}$ . Je mi jasné, že k řešení vede použití spektrálního rozkladu C (ten už mám, počítám pro konkrétní C) a pak pravidla o derivaci složené funkce a součinu, proto jsem výraz upravil na: $\psi(\mathbf{C})=\mathrm{tr}\left(\ln\left(\sqrt{\mathbf{C}}\right)\right)=\mathrm{tr}\left(\sum_{i=1}^s\ln\sqrt{\lambda_i}\mathbf{P}_i\right)= \frac{1}{2}\left(\sum_{i=1}^s\ln\left(\lambda_i\right)\mathrm{tr}\mathbf{P}_i\right)$ , kde P jsou příslušné „eigenprojections“ (česky...?) a lambdy vlastní čísla. Umím derivovat: $\frac{\partial \lambda_i}{\partial \mathbf{C}}=\mathbf{P}_i^T$ a $\frac{\partial \mathrm{tr}\mathbf{C}}{\partial \mathbf{C}}=\mathbf{I}$ . Kdybych postupoval analogicky jako u skalárních funkcí, tak bych dostal: $\mathbf{S}=2\frac{\partial \psi(\mathbf{C})}{\partial \mathbf{C}}=2\cdot \frac{1}{2}\sum_{i=1}^s $\frac{1}{\lambda_i}\mathbf{P}_i^T \mathrm{tr}\mathbf{P}_i+\ln(\lambda_i)\mathbf{I}\frac{\partial \mathbf{P}_i}{\partial \mathbf{C}}$$ . Je toto vůbec správně a pokud ano, jak vyjádřit poslední derivaci? Snad jsem to napsal srozumitelně, vyznáte se v tom někdo?

EDIT: Pokud je to až sem správně, tak mám asi vyhráno, protože vztah 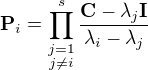$\mathbf{P}_i=\prod_{\substack{j=1 \\ j \neq i}}^s\frac{\mathbf{C}-\lambda_j \mathbf{I}}{\lambda_i-\lambda_j}$ už bych zderivovat dokázal...

FliegenderZirkus

Vyřešeno. Pokud by to někoho zajímalo, tak vzorové řešení využívá toho, že C je symetrický a dále se předpokládá, že má jednoduchá vlastní čísla. Pak totiž platí 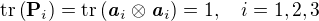$\mathrm{tr}\left(\mathbf{P}_i\right)=\mathrm{tr}\left(\textbf{\textit{a}}_i\otimes \textbf{\textit{a}}_i\right)=1,\quad i=1,2,3$ , kde a_i jsou vlastní vektory
$\psi(\mathbf{C})&=\mathrm{tr}\left(\ln\left(\sqrt{\mathbf{C}}\right)\right)=\mathrm{tr}\left(\sum_{i=1}^s\ln\sqrt{\lambda_i}\mathbf{P}_i\right)= \frac{1}{2}\left(\sum_{i=1}^s\ln\left(\lambda_i\right)\mathrm{tr}\mathbf{P}_i\right)=\frac{1}{2}\left(\sum_{i=1}^3\ln\left(\lambda_i\right)\right)=\\ &=\frac{1}{2} \ln\left(\lambda_1\lambda_2\lambda_3\right)=\frac{1}{2}\left( \ln\mathrm{III}_{\textbf{C}}\right)$ , kde III_C je třetí hlavní invariant, pro který platí $\frac{\partial \mathrm{III}_{\textbf{C}}}{\partial \textbf{C}}=\mathrm{III}_{\textbf{C}}\textbf{C}^{-1}$ .
Po derivaci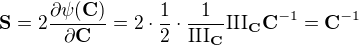
$\mathbf{S}=2\frac{\partial \psi(\mathbf{C})}{\partial \mathbf{C}}=2\cdot \frac{1}{2}\cdot\frac{1}{\mathrm{III}_{\textbf{C}}}\mathrm{III}_{\textbf{C}}\textbf{C}^{-1}=\textbf{C}^{-1}$

Z nějakého důvodu prý tento výsledek platí i pokud by vlastní čísla nebyla jednoduchá. Můj postup nakonec taky vede k cíli, ale zbytečně složitě.

Matematické Fórum

#1 10. 07. 2012 22:28 — Editoval FliegenderZirkus (10. 07. 2012 22:53)

Derivace tenzorové funkce

#2 11. 07. 2012 18:43 — Editoval FliegenderZirkus (11. 07. 2012 18:44)

Re: Derivace tenzorové funkce

Zápatí