Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » non- singular matrices (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 07. 2012 06:05
- stuart clark

- Příspěvky: 1015
- Reputace: 7
non- singular matrices
If  is a
is a 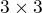 matrices with entries are from the set
matrices with entries are from the set  . Then total number of Non- Singular matrices
. Then total number of Non- Singular matrices  is
is
Offline
- (téma jako vyřešené označil(a) byk7)
#2 14. 07. 2012 10:39 — Editoval vanok (14. 07. 2012 21:48)
Re: non- singular matrices
Hi ↑ stuart clark:,
1) The total number of all possible matrices is  .
.
2) By considering the linear dependence of the columns of a matrix, we obtain the total number of all singular matrices is 
3) The total number of all regular matrices is

Edit: A correction of an oversight and addition of details.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 14. 07. 2012 20:47 — Editoval anes (14. 07. 2012 20:48)
Re: non- singular matrices
↑ vanok:
I understand that in step 2 you consider all matrices with 2nd row being multiple of the first (and vice versa, since there's no 0 involved), 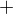 matrices with 3rd and 1st row being multiples,
matrices with 3rd and 1st row being multiples,  matrices, where all rows are multiples of each other, that you've counted twice in previous cases. I suppose at this point you forgot to count the matrices "sharing" only the 2nd and 3rd row. That should add another
matrices, where all rows are multiples of each other, that you've counted twice in previous cases. I suppose at this point you forgot to count the matrices "sharing" only the 2nd and 3rd row. That should add another  to the brackets.
to the brackets.
Let's take a look from the point of constructing a non-singular matrix.
We have  picks for the first row (there's no worry about a row of zeroes).
picks for the first row (there's no worry about a row of zeroes).
Having picked first row in any way, for the second row we have  options. The
options. The 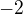 corresponds to
corresponds to  multiples of the first row, which are foridden.
multiples of the first row, which are foridden.
For the third row we have  options. The 4 corresponds to
options. The 4 corresponds to  multiples of first and second row. It's easy to check that there is no other combination of the first two rows that we'd need to worry about.
multiples of first and second row. It's easy to check that there is no other combination of the first two rows that we'd need to worry about.
So altogether we should have  different non-singular matrices.
different non-singular matrices.
Offline
#4 14. 07. 2012 21:53
Re: non- singular matrices
Hi ↑ anes:,
Thank you, I completed my oversight.
Obviously, both methods give the same answer.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » non- singular matrices (TOTO TÉMA JE VYŘEŠENÉ)
 matrices the second column of which is one
matrices the second column of which is one 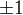 a multiple of the first column and and the third column is whatever
a multiple of the first column and and the third column is whatever matrix with the second column is one
matrix with the second column is one  matrices, column of which the sum second and third is one
matrices, column of which the sum second and third is one  multiple of the first one.
multiple of the first one.