Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Graf, hranově tranz. + není vrcholově tranz., pak bipartitní (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 07. 2012 22:25 — Editoval Andrejka3 (25. 07. 2012 08:46)
Graf, hranově tranz. + není vrcholově tranz., pak bipartitní
Ahoj,
Příklad zní.
Je-li graf 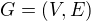 hranově tranzitiví a zároveň není vrcholově tranzitivní, pak je bipartitní.
hranově tranzitiví a zároveň není vrcholově tranzitivní, pak je bipartitní.
Dokaž.
Umím to dokázat pro případ, kdy graf nemá vrchol stupně nula.
Můj důkaz:
Je 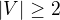 , jinak by byl graf triviálně vrcholově tranzitivní.
, jinak by byl graf triviálně vrcholově tranzitivní.
Volme 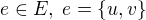 . To udělat mohu, protože kdyby
. To udělat mohu, protože kdyby  , pak by všechny vrcholy měly nulový stupeň a navíc by byl graf vrcholově tranzitivní.
, pak by všechny vrcholy měly nulový stupeň a navíc by byl graf vrcholově tranzitivní.
Označme: ,
,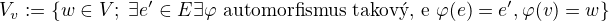 ,
,
kde 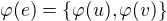 .
.
Chci ukázat, že tyto (neprázdné) množiny jsou disjunktním rozkladem  :
:
Graf je vrcholově tranzitivní, proto je 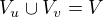 .
.
Kdyby 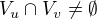 , pak volím
, pak volím 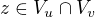 .
.
Chci ukázat, že tento předpoklad vede ke sporu s tím, že  není vrcholově tranzitivní.
není vrcholově tranzitivní.
Pro libovolné dva vrcholy  platí - jsou buďto oba v jedné z dvou množin
platí - jsou buďto oba v jedné z dvou množin 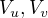 , pak ale existuje automorfismus, který zobrazuje BÚNO
, pak ale existuje automorfismus, který zobrazuje BÚNO 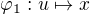 a jiný,
a jiný, 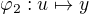 . Pak
. Pak 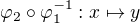 a je to automorfismus.
a je to automorfismus.
Pokud jsou naopak oba vrcholy v jiné z dvou množin, je BÚNO 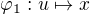 ,
, 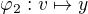 , ale mame
, ale mame 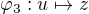 a
a  , odkud
, odkud 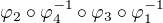 je automorfismus
je automorfismus  , který zobrazuje
, který zobrazuje  na
na  .
. je vrcholově tranzitivní, což je spor s předpokladem, že není. Musí tedy být
je vrcholově tranzitivní, což je spor s předpokladem, že není. Musí tedy být 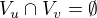 , a je tedy
, a je tedy  bipartitní.
bipartitní.
Jak to mám udělat, pokud existuje vrchol nenulového stupně? Nebo pak tvrzení neplatí?
Díky,
A.
PS: definice: 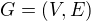 graf
graf
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 25. 07. 2012 08:35 — Editoval Andrejka3 (25. 07. 2012 08:43)
Re: Graf, hranově tranz. + není vrcholově tranz., pak bipartitní
Myslím, že mám protipříklad:
Graf s vrcholy 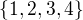 , kde vrcholy 1,2,3 tvoří kružnici a vrchol 4 má nulový stupeň. Takový graf je hranově tranzitivní, není vrcholově tranzitivní a není bipartitní.
, kde vrcholy 1,2,3 tvoří kružnici a vrchol 4 má nulový stupeň. Takový graf je hranově tranzitivní, není vrcholově tranzitivní a není bipartitní.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Graf, hranově tranz. + není vrcholově tranz., pak bipartitní (TOTO TÉMA JE VYŘEŠENÉ)
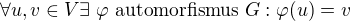 .
. ,
, 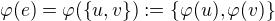 .
. .
. je automorfismus
je automorfismus 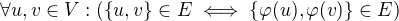 .
. , disjunktní rozklad
, disjunktní rozklad 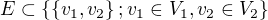
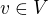 .
.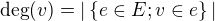 .
. .
.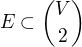 , nazveme grafem.
, nazveme grafem.  značí množinu všech dvouprvkových podmnožin
značí množinu všech dvouprvkových podmnožin  se rika mnozina hran.
se rika mnozina hran.