Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 08. 2012 09:54 — Editoval Dunemaster (06. 04. 2021 19:33)
- Dunemaster
- Host
-
-
#2 01. 08. 2012 14:06 — Editoval Honzc (01. 08. 2012 14:08)
Re: -
↑ Dunemaster:
To asi není moc těžké. Protože se čísla nemohou opakovat a nezáleží na pořadí, pak jejich počet je dán jako kombinace k-té třídy z n prvků , tedy počet 
A praktiké vyjádření také nebude složité.
Třeba pro n=5, k=3 to bude rozepsáno nejjednodušeji takto: (10 možností)
123
124
125
134
135
145
234
235
245
345
Offline
#3 01. 08. 2012 16:01 Příspěvek uživatele Dunemaster byl skryt uživatelem Dunemaster.
#4 01. 08. 2012 16:23
Re: -
↑ Dunemaster:
Zajímavý příklad.
Přeformuluji to:
Mějme množinu  o
o  prvcích. Mějme číslo
prvcích. Mějme číslo  ,
,  . Kolik existuje uspořádání
. Kolik existuje uspořádání  na množině
na množině  (všech k-tic množiny
(všech k-tic množiny  ) splňující:
) splňující: ,
,
kde  je relace bezprostředního předchůdce uspořádání
je relace bezprostředního předchůdce uspořádání  .
.
Možná tato formulace není vhodná k řešení, ale zdá se mi srozumitelná.
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 01. 08. 2012 17:26 — Editoval vanok (02. 08. 2012 13:16)
Re: -
pokusy
n=3
mozna jedina postupnost aku vyzadujes
(1,2,3)... ma dlzku 1
n=4
(a,bc) (a,b,d)
(a,b,c) (a,c,d)
(a,b,c) (b,c,d)
cize kazdy postupnosti clen ma troch moznych nasledovnikov
( vizualicia "typ fraktalneho stromu" )
a kazdu pripustnu ( tie coi vyhovuju tvojej podmienke), mozme vyjadrit z poslednej uvahy pocet postupnosti dlzky k ( k nenulove prirodzene cislo)
n=5
(a,b,c) (a,b,d)
(a,b,c) (a,c,d)
(a,b,c) (b,c,d)
(a,b,c) (a,b,e)
(a,b,c) (a,c,e)
(a,b,c) (b,c,e)
kazdy clen postupnosti ma 6 moznych nasledovnikov
NA POKRACOVANIE
OTAZKY :napis typ problemu co ta doviedli k tejto problematike?
Da sa na takychto mnozinach prvkov definovat pojem vzdialenosti?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 01. 08. 2012 21:54 — Editoval check_drummer (02. 08. 2012 20:02)
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: -
Ahoj,
co mě napadlo: stará dobrá indukce.
Chceme vhodně uspořádat  prvků. Nechť pro jednoduchost je N:={1,..,n}. Budeme postupovat indukcí dle
prvků. Nechť pro jednoduchost je N:={1,..,n}. Budeme postupovat indukcí dle  . Zřejmé jsou případy
. Zřejmé jsou případy 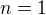 i
i  . V ostatních případech pro dané N rozdělme
. V ostatních případech pro dané N rozdělme  na množiny A a B, kde každá k-tice z A neobsahuje a každá k-tice z B obsahuje prvek n. Dle indukce lze A uspořádat a rovněž i B lze uspořádat - odstraníme ze všech k-tic v B prvek n, dle indukce ji uspořádáme a následně se přidáním prvku n k těmto k-1 ticím na korektnosti uspořádání nic nezmění.
na množiny A a B, kde každá k-tice z A neobsahuje a každá k-tice z B obsahuje prvek n. Dle indukce lze A uspořádat a rovněž i B lze uspořádat - odstraníme ze všech k-tic v B prvek n, dle indukce ji uspořádáme a následně se přidáním prvku n k těmto k-1 ticím na korektnosti uspořádání nic nezmění.
Zbývá dořešit otázku, jak napojit uspořádané A na uspořádané B. To je ale jednoduché - lze totitž jednoduše dosáhnout toho, aby první nebo poslední k-tice v A i v B byla taková jakou chceme - jednoduše zpermutujeme vhodně prvky množiny, ze které k-tice vybíráme. A i B lze ovšem zpermutovat odlišně a tak lze dosáhnout toho, že poslední prvek A je {1,2,..,k-1,k} a první prvek B je {1,2,..,k-1,n}, čímž je úloha vyřešena.
Snad tam není někde slabé místo.
"Máte úhel beta." "No to nemám."
Offline
#7 02. 08. 2012 07:22
Re: -
↑ Dunemaster:
Píšeš ...aby se každé následující lišilo právě v jednom čísle !!!...
A co ti brání to co jsem napsal
123
124
125
134
135
145
234
235
245
345
srovnat takto:
123
124
125
135
134
145
245
235
234
345
Offline
#8 02. 08. 2012 12:34 — Editoval Andrejka3 (02. 08. 2012 12:35)
Re: -
pro dané N rozdělme N na množiny A a B, kde každá k-tice z A neobsahuje a každá k-tice z B obsahuje prvek n.
Jak rozdělit N tak, jak píšeš? Nebo píšeš o rozdělení  = množiny všech k prvkových podmnožin množiny N - na A a B, kde ...
= množiny všech k prvkových podmnožin množiny N - na A a B, kde ...
Ráda si ten důkaz projdu později, teď musím pryč, ale narazila jsem na problém výše.
↑ Honzc:
Jak víš, že takových uspořádání je právě  ?
?
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 02. 08. 2012 13:28 — Editoval vanok (02. 08. 2012 13:38)
Re: -
↑ vanok:
Pripad typu (3,n)
Prva veta:
V kazdej pripustnej nekonecnej Dunemaster-ovej postupnosti , ktorej prvy prvok je (a,b,c)
Dokazte!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 02. 08. 2012 20:01
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: -
↑ Andrejka3:
Ahoj, omlouvám se, jde o rozdělení množiny všech k prvkových podmnožin množiny N - na A a B. Opravím to.
"Máte úhel beta." "No to nemám."
Offline
#11 03. 08. 2012 10:01 — Editoval Andrejka3 (03. 08. 2012 10:02)
Re: -
↑ check_drummer:
Ahoj,
je to elegantní důkaz, takový polokonstrukční toho, že vždy existuje aspoň jedno takové uspořádání.
Tím, že indukce případ 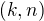 převedla na již vyřešené případy
převedla na již vyřešené případy  a
a  .
.
Otázka ale byla též, kolik takových uspořádání existuje. Doteď mi nebylo jasné, zda to lze vždy udělat, teď už je.
Díky.
↑ vanok:
Ahoj, na předchozí příspěvek o stromech neumím reagovat, protože ještě stromy neznám.
V tomto příspěvku mě zaráží, že píšeš o nekonečné Dunemasterovské posloupnosti, v případě , kdy by měla každá posloupnost mít
, kdy by měla každá posloupnost mít  členů a ty členové jsou tří prvkové podmnožiny množiny
členů a ty členové jsou tří prvkové podmnožiny množiny  .
.
Hezký víkend všem.
What does a drowning number theorist say?
'log log log log ...'
Offline
#12 03. 08. 2012 11:46 — Editoval vanok (03. 08. 2012 11:47)
Re: -
↑ Andrejka3:
Nekonecna postupnost v mojej interpretaci je skutocna postupnost 
Dunemaster-ovov podmienkov tykajuca sa dvoch susednych clenov:
"  su pripustne v zmysle Dunemaster-a"
su pripustne v zmysle Dunemaster-a"
Napriklad v situacii (k,n)=(3,5)
mame tuto Dunemaster-ovu (periodicku) postupnost
(1,2,3);(1,2,4);(1,2,3);(1,2,4);...
alebo
(1,2,3);(1,2,4);(1,2,5);(1,2,4);(1,4, 5);...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 13. 08. 2012 01:37 — Editoval check_drummer (13. 08. 2012 09:18)
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: -
↑ Andrejka3:
Ahoj, ze zadání úlohy mi neplyne, že bychom měli zkoumat, kolik takových uspořádání existuje, ale jen to, zda vůbec nějaká existuje (otázka "Jak je dát do posloupnosti" navíc vyžaduje konstrukční důkaz). Nicméně zjistit tento počet by bylo jistě zajímavé - ale obávám se, že sestavení byť rekurentní rovnice nebude snadné. Ale víme (viz existenční důkaz), že tento počet bude aspoň n!, dokonce násobek n! - každá "třída" řešení má n! prvků. Možná by bylo zajímavé tento počet pro malá n,k experimentálně zjistit - tedy jako f(n,k).n! a bylo by zajímavé zkoumat f(n,k).
Edit: Další poznatek: každou přípustnou posloupnost lze začít libovolnou k-ticí a jako druhou použít další libovolnou přípustnou k-tci, takových je  . Tedy hledaný počet je jak násobkem n!, tak i násobkem
. Tedy hledaný počet je jak násobkem n!, tak i násobkem  .
.
Ještě mě napadlo, že další omezení úlohy by mohlo spočívat v tom, že první a poslední k-tice se musí liší rovněž jen v jednom prvku. Pak by můj existenční důkaz šel s mírnou modifikací rovněž použít - permutace by se musela volit "restriktivněji". Rovněž zde by bylo zajímavé hledat počet takových uspořádání.
"Máte úhel beta." "No to nemám."
Offline
#14 13. 08. 2012 01:55
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: -
↑ vanok:
Ahoj, pod přípustnou nekonečnou D-posloupností (D jako Dunemaster) máš na mysli, že použiješ všechny k-tice v nějakém pořadí a následně toto pořadí stále opakuješ? Tj. posloupnost je vždy  periodická? Pokud ne, pak lze volit např. (1,2,3),(1,2,4),(1,2,5),(1,2,4),(1,2,5),... Pokud ano, pak se vlastně jedná o to mé zobecnění, kdy pro první a poslední člen této posloupnosti musí rovněž platit, že se liší v jednom členu. A Tvé tvrzení tedy říká, že pro k=3 jde o tentýž případ jako původní problém - to je zajímavé. Ale příklad, který uvedl Honzc je dle mého protipříklad, díky kterému Tvé tvrzení neplatí...
periodická? Pokud ne, pak lze volit např. (1,2,3),(1,2,4),(1,2,5),(1,2,4),(1,2,5),... Pokud ano, pak se vlastně jedná o to mé zobecnění, kdy pro první a poslední člen této posloupnosti musí rovněž platit, že se liší v jednom členu. A Tvé tvrzení tedy říká, že pro k=3 jde o tentýž případ jako původní problém - to je zajímavé. Ale příklad, který uvedl Honzc je dle mého protipříklad, díky kterému Tvé tvrzení neplatí...
"Máte úhel beta." "No to nemám."
Offline
#15 13. 08. 2012 10:42 — Editoval vanok (13. 08. 2012 10:45)
Re: -
Ahoj ↑ check_drummer:,
Nie ta periodicita nie je nutna, podla mna, to som dal len ako priklad takej nekonecnej postupnosti.
Otvorena otazka, ake su mozne dlzky postupnosti, aby sa znovu objavil jej prvy clen?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 13. 08. 2012 15:01
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: -
↑ vanok:
Ahoj, podle mého jsou všechny délky kromě 2 možné (povolíme-li, aby se členy posloupnosti opakovaly - což je nejspíš povoleno, protože zkoumáme případ, kdy se první člen objeví znovu, tj. opakuje se) pro k<n a lichou délku a navíc pro n>2 a sudou délku. Např. posloupnost délky 3 získáme jako (1,2,X), (1,3,X), (1,2,X) a posloupnost délky 4 jako (1,2,X), (1,3,X), (2,3,X), (1,2,X), kde X jsou prvky doplňující k-tici. Následně můžeme postupovat indukcí a podposloupnost A1 o jednom členu rozšířit na posloupnost A1,..,A1 o lichém počtu členů.
"Máte úhel beta." "No to nemám."
Offline
#17 13. 08. 2012 15:49
Re: -
Ano ↑ check_drummer:, aj ja som to nasiel ako ty.
Mozno sa neskor vratim este k tomuto problemu.
Da sa na tom iste este pobavit. ... Napr v konecnych telesach.
Pekne popoludnie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


 take ze
take ze 