Matematické Fórum

gladiator01

Určete intervaly v nichž je fce f ryze monotonní
1) $f(x)=\frac{x}{ln^2 x}$

2) $f(x)=2x*arccot x+ln(1+{x^2})-\pi x$

3) $f(x)=x(1-lnx)^2$ u tohoto kdyby někdo napsal i postup derivování, nějak mi to nechce vyjít

prosím o jakoukoliv radu, nejlépe nástin řešení

Marian · 14. 11. 2008 15:34

↑ gladiator01:
Bude ti k tomu stačit znaménko první derivace. Ale tak jak formuluješ svůj dotaz tak bych řekl spíše, že se jedná o rozkaz. Derivovat asi budeš umět, takže byl bych rád, kdybys uvedl také nějaké své návrhy k řešení této úlohy.

Pomoct si třeba můžeš také zde, záložka diferenciální počet.

gladiator01

↑ Marian:

omlouvám se jestli můj dotaz vyzněl jako rozkaz, to nebyl úmysl, díky za ten odkaz

gladiator01

↑ Marian:
ad 1) Vyšly mi tedy stacionární body pro první derivace 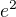$e^2$ a pro druhou derivace $e^3$

co dál?
jak mám zjistit ty intervaly, kdy fce klesá a roste?

ve skriptech mam výsledek roste na int. (0,1)U(e^2, nekonečno) a klesá (1,e^2) (nevím jestli to je správně, bývají tam chyby) - mohl by mi to někdo vysvětlit proč to tak je?

ttopi · 14. 11. 2008 17:50

Rozkazovací věta končí vykřičníkem, čili toto nemůže být rozkaz.

gladiator01 · 15. 11. 2008 14:00

mohl by prosím vás někdo spočítat tu trojku? dík

lukaszh

↑ gladiator01:
Najprv si upravím funkciu:
$f(x)=x(1-\ln x)^2=x(1-2\ln x+\ln^2x)=\boxed{x-2x\ln x+x\ln^2x}$
Teraz môžem derivovať postupne:
$\frac{\textrm{d}f(x)}{\textrm{d}x}=\frac{\textrm{d}}{\textrm{d}x}(x)+\frac{\textrm{d}}{\textrm{d}x}(-2x\ln x)+\frac{\textrm{d}}{\textrm{d}x}(x\ln^2x)$
Rozpíšem si derivácie...
$\frac{\textrm{d}}{\textrm{d}x}(x)=1\nl\frac{\textrm{d}}{\textrm{d}x}(-2x\ln x)=-2\frac{\textrm{d}}{\textrm{d}x}(x\ln x)=-2$1\cdot\ln x+x\cdot\frac{1}{x}$=-2(\ln x+1)\nl\frac{\textrm{d}}{\textrm{d}x}(x\ln^2x)=\ln^2x+x$2\ln x\cdot\frac{1}{x}$=\ln^2x+2\ln x$
... a teraz všetky sčítam a upravím na prijateľný tvar:
$\frac{\textrm{d}f(x)}{\textrm{d}x}=1-2(\ln x+1)+\ln^2x+2\ln x=1-2\ln x-2+\ln^2x+2\ln x=\boxed{\ln^2x-1}$

gladiator01 · 15. 11. 2008 15:24

↑ lukaszh: dík

Jakub Pištěk · 15. 11. 2008 16:35

ten příklad číslo dvě mi vyšel roustoucí(-nekonečno,0) vyšlo vám to taky tak?

gladiator01 · 15. 11. 2008 16:40

↑ Jakub Pištěk:
podle výsledků ve skriptech by to mělo být správně

Jakub Pištěk · 15. 11. 2008 17:18

u té třetí mi vyšlo že je roustoucí intervalu (0, cca 0.36)U(e, +nekonečno) to 0,36 jsem zjistil že jsem zadal tu funkci do programu který vypíše graf a pak jsem zkoušel zadávat kolik se rovna ln(0.36)^2 hranice kdy je to ještě větší než nula jsem zjistil kolem té 0.36 nevíte jak bych tento pod podezřelý z extrému našel kdybych tento příklad dostal na papír v písemce.

gladiator01 · 15. 11. 2008 17:29

↑ Jakub Pištěk:
mě teda vyšlo z tý derivace co spočítal lukaszh že je rostoucí v (0, 1/e) U (e, nekonečno), nevím jestli jsem to spočítala správně (ale mělo by to takhle být).

Jakub Pištěk · 15. 11. 2008 17:58

jo to je ono to 1/e je přibližně 0.36 jen mě zajímá jak si to z hlavy odvodit když vidim tenhle příklad na papíře a počítám ho na zápočtový písemce

gladiator01 · 15. 11. 2008 18:19

no když si rozložíš to ${\ln^2x-1}$ tak ti vyjde (lnx-1)(lnx+1)
ty závorky položíš k nule (lnx-1)=0 a (lnx+1)=0 --> lnx=1 a lnx=-1 --> x=e a x=1/e. Já nevim jak jsi to počítal ale takhle jsem to teda pochopila, že se to má dělat.

Jakub Pištěk · 15. 11. 2008 18:35

jo díky už to chápu :)

Matematické Fórum

#1 14. 11. 2008 15:29 — Editoval gladiator01 (15. 11. 2008 11:24)

derivace - monotonnost fce

#2 14. 11. 2008 15:34

Re: derivace - monotonnost fce

#3 14. 11. 2008 15:37 — Editoval gladiator01 (14. 11. 2008 15:42)

Re: derivace - monotonnost fce

#4 14. 11. 2008 17:24 — Editoval gladiator01 (14. 11. 2008 17:56)

Re: derivace - monotonnost fce

#5 14. 11. 2008 17:50

Re: derivace - monotonnost fce

#6 15. 11. 2008 14:00

Re: derivace - monotonnost fce

#7 15. 11. 2008 14:24 — Editoval lukaszh (15. 11. 2008 14:25)

Re: derivace - monotonnost fce

#8 15. 11. 2008 15:24

Re: derivace - monotonnost fce

#9 15. 11. 2008 16:35

Re: derivace - monotonnost fce

#10 15. 11. 2008 16:40

Re: derivace - monotonnost fce

#11 15. 11. 2008 17:18

Re: derivace - monotonnost fce

#12 15. 11. 2008 17:29

Re: derivace - monotonnost fce

#13 15. 11. 2008 17:58

Re: derivace - monotonnost fce

#14 15. 11. 2008 18:19

Re: derivace - monotonnost fce

#15 15. 11. 2008 18:35

Re: derivace - monotonnost fce

Zápatí