Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 08. 2012 16:20 — Editoval vanok (13. 08. 2012 16:21)
zlozene cislo
Mala pradzninova uloha:
Dokazte, ze v akejkolvek ciselnej sustave je zlozene cislo.
je zlozene cislo.
A este jedna trochu tazsia:
Dokazte, ze sucin 5-tych po sebe iducich positivnych ( ) cisiel nie je nikdy stvorec nejakeho celeho cisla.
) cisiel nie je nikdy stvorec nejakeho celeho cisla.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 13. 08. 2012 18:42
Offline
#3 13. 08. 2012 18:53 — Editoval vanok (13. 08. 2012 23:21)
Re: zlozene cislo
Ahoj ↑ jarrro:,
Ano to je klucova idea tohto stredoskolskeho cvicenia.
Dufajme, ze kazdy stredoskolak ju dokaze dokazat a ze je schopny redigovat kompletny podrobny dokaz
Ide o pouzitie uzitocnej Argand-ovej identity.
Pridavam tu uzitocnu stranu z pozoruhodnyny identitamy
http://fr.wikipedia.org/wiki/Identit%C3 … d.27Argand
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 20. 08. 2012 20:24 — Editoval vanok (20. 08. 2012 23:13)
Re: zlozene cislo
Pozdravujem.
Ako vidim, toto cvicenie
Dokazte, ze sucin 5-tych po sebe iducich positivnych ( ) cisiel nie je nikdy stvorec nejakeho celeho cisla.
) cisiel nie je nikdy stvorec nejakeho celeho cisla.
sa este nepohlo.
Tak davam navod, na jedno jeho mozne riesenie.
Najprv pozorovanie
Cislo 
je jasne ze toto cislo ma
dva alebo tri cleny ktore obsahuju mocniny cisla 2
jeden alebo dva cleny ktore obsahuju mocniny cisla 3
jeden clen clen ktory obsahuje mocninu cisla 5
a najviac jeden clen pre kazde prvocislo striktne vadcie ako 5.
Teraz predpokladajme, ze  je dokonaly stvorec
je dokonaly stvorec
to znamena, ze kazde z cisiel  je formy
je formy  kde
kde  a
a
 je formy
je formy kde
kde 
Teraz, treba studovat N, podla hodnot  , kazdeho
, kazdeho  kde
kde 
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 21. 08. 2012 18:35
Re: zlozene cislo
pomoc pokracovanie
Lahko prideme k tomuto vysledku
Kazde z cisiel  musi mat jednu z tychto foriem
musi mat jednu z tychto foriem
Akoze mame 5 cisiel  tak dva cisla musia mat taku istu formu.( vdaka Diriclet-ovmu priehradkovemu principu)
tak dva cisla musia mat taku istu formu.( vdaka Diriclet-ovmu priehradkovemu principu)
Dufam, ze teraz uz niekto nam da uplny dokaz.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 21. 08. 2012 19:38
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: zlozene cislo
↑ vanok:
Ahoj, proč se v daném čísle vyskytují 5 a 7 v sudé mocnině? Děkuji.
"Máte úhel beta." "No to nemám."
Offline
#7 21. 08. 2012 19:57
Re: zlozene cislo
↑ check_drummer:
Pretože medzi číslami  je práve jedno alebo žiadne deliteľné prvočíslom
je práve jedno alebo žiadne deliteľné prvočíslom  . Nakoľko je podľa predpokladu ich súčin štvorec, tak potom rovno
. Nakoľko je podľa predpokladu ich súčin štvorec, tak potom rovno 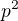 delí to príslušné číslo.
delí to príslušné číslo.
1^6 - 2^6 + 3^6 = 666
Offline
#8 21. 08. 2012 22:41
Re: zlozene cislo
↑ check_drummer:
pozdravujem,
kolega ↑ BakyX: to dokonale objasnil.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 22. 08. 2012 01:31 — Editoval anes (22. 08. 2012 11:20)
Re: zlozene cislo
Ahoj, promiň vanok, že Ti tu trochu nabourám pečlivě budované téma. To řešení, které jsi už téměř dotáhl, je asi takové nejpřirozenější a v principu nenavrhnu nic jiného, ale přijde mi to jako hezký příklad situace, kdy drobná změna zápisu usnadní práci.
EDIT: Tak horké to s tím usnadněním nebude, viz ↑ BakyX:.
Jinak si myslím, že to zakončení důkazu je v mé varianě trochu jiné, než kam vede postup ↑ vanok:, tak tam ten závěrečný argument může dodat ještě někdo jiný :)
Mimochodem ta věta "Tak davam navod, na jedno jeho mozne riesenie" byl jenom takový disclaimer, že to může jít i snáz, nebo máš v záloze i jiné postupy?
Offline
#10 22. 08. 2012 02:26
Offline
#11 22. 08. 2012 11:18
Re: zlozene cislo
Offline
#12 22. 08. 2012 21:47
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: zlozene cislo
↑ BakyX:
Děkuji, přehlédl jsem poznámku, že předpokládáme, že jde o čtverec...
"Máte úhel beta." "No to nemám."
Offline


 je násobek 5, a dokonce také 25. Rozhodně se tedy bavíme o číslech větších než 20.
je násobek 5, a dokonce také 25. Rozhodně se tedy bavíme o číslech větších než 20.  o 2 místa pounout a přejít k
o 2 místa pounout a přejít k  .
. musí mít v prvočíselném rozkladu sudou mocninu u dvojky, u trojky i u všech dalších prvočísel. Kdyby totiž
musí mít v prvočíselném rozkladu sudou mocninu u dvojky, u trojky i u všech dalších prvočísel. Kdyby totiž  by byl lichý (tj. bez dvojky) a člen
by byl lichý (tj. bez dvojky) a člen  by dvojku obsahoval ve druhé mocnině. Celý součin by pak obsahoval dvojku v liché mocnině a nemohl by tvořit čtverec. Stejně se zdůvodní i ty další případy.
by dvojku obsahoval ve druhé mocnině. Celý součin by pak obsahoval dvojku v liché mocnině a nemohl by tvořit čtverec. Stejně se zdůvodní i ty další případy.  . Čtverec jakého čísla? Moc jich v úvahu nepřipadá, asi jen dvě:
. Čtverec jakého čísla? Moc jich v úvahu nepřipadá, asi jen dvě:
 .
. ) se ani s jedním netrefíme do hodnoty
) se ani s jedním netrefíme do hodnoty  , takže máme smůlu.
, takže máme smůlu. člen
člen  , čo je číslo, ktoré obsahuje dvojku v nepárnej mocnine :(
, čo je číslo, ktoré obsahuje dvojku v nepárnej mocnine :(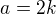 , kde
, kde  je liché, a jestli se zas nepletu, tak lichou mocninu vyrobí dokonce každé
je liché, a jestli se zas nepletu, tak lichou mocninu vyrobí dokonce každé  , kde
, kde  a
a  . Čas příspěvku mě snad trochu omlouvá, protože tohle jsem si zkusit ověřit mohl :)
. Čas příspěvku mě snad trochu omlouvá, protože tohle jsem si zkusit ověřit mohl :)