Matematické Fórum

PetrCNC · 22. 08. 2012 17:30

Potřebuji nasměrovat k vyřešení úlohy pro program na obrabění na CNC stroji, jde o kruhovou interpolaci. potřebuji zjístit dva body na středové přímce v kružnici. viz. obrázek, když znám hodnotu "a1" a "b1" a poloměr kružnice. Už mě někdo nasměroval na kvadratickou rovnici ale nevím jak do ní zapíšu hodnoty co znám.

Výsledkem by mělo být b2=0,522 a2=2,632 nejde mi o vysledek ale o vzorec jak k tomu dojít.

díky

rleg · 22. 08. 2012 18:09 — Editoval rleg (22. 08. 2012 18:14)

↑ PetrCNC:
Zdravím
pokud se nepletu, stačí k řešení použít pouze goniometrické a cyklometrické funkce.
Mělo by platit, že
$b_1=r\cdot\sin{\varphi} \nl b_2=r\cdot\cos{\varphi}\nl \varphi=\arcsin{\frac{b_1}{r}} \Rightarrow b_2=\cos {$\arcsin{\frac{b_1}{r}}$}$

nebo pokud to chceš kvadratickou rovnicí, tak by mělo platit, že
$b_1^2+b_2^2=r^2$

miso16211 · 22. 08. 2012 18:15

↑ rleg: pomocou Pytagorovej vety veľmi ľahko, učivo základnej školy

PetrCNC · 22. 08. 2012 20:15

↑ miso16211:Pravda, ale stejně mě udivuje že jeden prof. ing csc mi právě dnes radil kvadratickou rovnici ale prej že to není na hodinu udělat tohle řešení. jedná se tedy o načrtnutý trojuhelník, viz. obrázek. nechápu proč tam je to r2 , když do trojuhelniku nejak nezasahuje když nejde středem kružnice. Ale hlavně že to funguje. ale vzorec je přesně takto: $b_{2}=12-(\sqrt{r^{2}-b_{2}^{2}})$

PetrCNC · 22. 08. 2012 20:16

↑ rleg:taky děkuji za pomoc teď už to jen nějak zapsat do programu

jelena · 22. 08. 2012 21:10

↑ PetrCNC:

Zdravím,

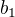a) ve vzorci $b_{2}=12-(\sqrt{r^{2}-b_{2}^{2}})$ je překlep, má být $b_1$ úplně na závěr.

b) podle obrázku v příspěvku 4 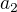$b_2$ , $a_2$ jsou vzdálenosti od nulového bodu O "měřeno nalevo". Proto délku $b_2$ máme jako rozdíl celého poloměru $r$ (12 cm) a pomocné délky SB, kterou vypočteme z pravoúhlého trojúhelníku (to počítá i kolega rleg).

Proto nejdřív spočteme "pomocnou délku" $|SB|=\sqrt{r^2-b_1^2}$ (S-střed kružnice, B je bod, ve kterém je ? nad $b_2$ ), potom dosadíme do:
$|OB|=b_{2}=r-|SB|=r-\sqrt{r^{2}-b_{1}^{2}}=12-\sqrt{12^{2}-3,5^{2}}$

Podaří se zorientovat?

Téma patří do jiné sekce, přesunu do Ostatního.

PetrCNC · 23. 08. 2012 05:55

↑ jelena: díky teď to má hlavu i patu, za vyřešení a pomoc posilám 20kč, když je to tedy učivo zakl. školy:)

Honzc · 23. 08. 2012 06:23

↑ PetrCNC:
Jenom pane kolego nezapomeň na to, že v tomto případě bude mít souřadnice daného bodu na kružnici záporné znaménko.
Tedy B[x,z] = [3.5,-|OB|]

PetrCNC · 23. 08. 2012 09:16

↑ Honzc:to vím, ale v CNC programu je souřadnicoví systém kapku jiný. Znaménko přiřadím až po veškerých výpočtech.

jelena · 23. 08. 2012 12:11

↑ PetrCNC:

také děkuji i za SMS.

když je to tedy učivo zakl. školy:)

:-) znáš vtip o úderu kladivem za 50 dolarů?

A jinak na rady kolegy Honzce bych brala velký ohled, neb je praktický strojař (a nejen), kolegu zdravím.

PetrCNC · 23. 08. 2012 12:56

↑ jelena:vtip neznám mužeš napsat. Já myslel že tady jsou spíše z oboru matematiky:) která ovšem zasahuje téměř do všech oborů. za sms není zač, není dobré rady zadarmo:)

Matematické Fórum

#1 22. 08. 2012 17:30

Výpočet bodu v kruhové interpolaci.

#2 22. 08. 2012 18:09 — Editoval rleg (22. 08. 2012 18:14)

Re: Výpočet bodu v kruhové interpolaci.

#3 22. 08. 2012 18:15

Re: Výpočet bodu v kruhové interpolaci.

#4 22. 08. 2012 20:15

Re: Výpočet bodu v kruhové interpolaci.

#5 22. 08. 2012 20:16

Re: Výpočet bodu v kruhové interpolaci.

#6 22. 08. 2012 21:10

Re: Výpočet bodu v kruhové interpolaci.

#7 23. 08. 2012 05:55

Re: Výpočet bodu v kruhové interpolaci.

#8 23. 08. 2012 06:23

Re: Výpočet bodu v kruhové interpolaci.

#9 23. 08. 2012 09:16

Re: Výpočet bodu v kruhové interpolaci.

#10 23. 08. 2012 12:11

Re: Výpočet bodu v kruhové interpolaci.

#11 23. 08. 2012 12:56

Re: Výpočet bodu v kruhové interpolaci.

Zápatí