Matematické Fórum

mc_wave · 24. 08. 2012 01:34

Pořád nějak nemůžu pochopit kdy se v dilataci času používá jaký vzorec...
Mohl by mi někdo to nějak popsat?

$http://www.matweb.cz/cgi-bin/mathtex.cgi?\dpi{140}\gammacorrection{1}\parstyle\begin{align*}\usepackage[czech]{babel}%20\Delta%20t=\frac{\Delta%20t_0}{\sqrt{1-\frac{v^2}{c^2}}}\end{align*}$

$http://www.matweb.cz/cgi-bin/mathtex.cgi?\dpi{140}\gammacorrection{1}\parstyle\begin{align*}\usepackage[czech]{babel}%20t=t0\cdot\sqrt{1-\frac{v^{2}}{c^{2}}}\end{align*}$

Mirgeee

Víš, co ten vzorec znamená? Která doba trvání určitého děje je větší: ta v klidové soustavě S', nebo ta v soustavě S, která se vzhledem k S' pohybuje?
Hodiny, které se vzhledem k pozorovateli pohybují, jdu vzhledem k tomuto pozorovateli pomaleji než hodiny, které se nepohybují, viď?
Označme si $\Delta t$ trvání děje v pohybující se soustavě, $\Delta t'$ trvání děje pro nás - pozorovatele v klidu.
A co ten výraz 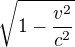$\sqrt{1-\frac{v^2}{c^2}}$ ? c > v, viď, takže ten výraz bude nabývat hodnoty od nuly do jedné.
Teď máme dva časy, t > t', a výraz v intervalu (0;1). Takže na kterou stranu ten výraz patří?

Autor skryl část textu. Zobrazit/skrýt!

Tady si můžeš prohlédnout odvození, a tady video.

TomF · 24. 08. 2012 11:06 — Editoval TomF (24. 08. 2012 11:08)

Ahoj, také se přidám :-)
jde prostě o to, že v jedné rovnici je vyjádřený čas pohybujícíse soustavy z pohledu klidové soustavy a v druhé je zpětně vyjádřeno, jak by se čas pohybující soustavy jevil, kdyby se nepohybovala, přičemž počítáme s časem z první rovnice:
pro jednoduchost napíšu $\gamma =\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$
potom
$t=t_{0}*\gamma$
$t_{0}=\frac{t}{\gamma }=t*\sqrt{1-\frac{v^{2}}{c^{2}}}$

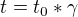
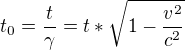
a pro doplnění a lepší pochopení zjednodušenou Lorentzovu transformaci,
kde x,y,z jsou prostorové souřadnice, u je rychlost ve směru x, a t je čas,
čárkovaně pohybujícíse soustava...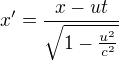

$x'=\frac{x-ut}{\sqrt{1-\frac{u^{2}}{c^{2}}}}$
$y'=y$
$z'=z$
$t'=\frac{t-\frac{u}{c^{2}}x}{\sqrt{1-\frac{u^{2}}{c^{2}}}}$

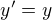
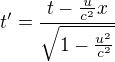
můžeš si všimnout, že pro vyjádření x,y,z,t stačí jen vyměnit čárkování a otočit znaménko rychlosti
tady http://www.forum.matweb.cz/viewtopic.php?id=48828 Pietro krásně popsal Michelsonův-Morleyův experiment a obecnou Lorentzovu transformaci, tak můžeš také prostudovat..

Mirgeee · 24. 08. 2012 12:54

Pokud jsi o Lorentzově transformaci neslyšel: Lorentzova transformace je taková matematická pomůcka, která nám ze známých souřadnic x, y, z a t umožní vypočítat x', y', z' a t'. Můžeš si ty vzorce zkusit sám odvodit, není to nic těžkého. Např. pro odvození souřadnice x' si nakresli obrázek těch dvou soustav a použij vztah pro kontrakci délky 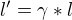$l'=\gamma *l$ ... S tím časem to taky nebude nic složitého.

Matematické Fórum

#1 24. 08. 2012 01:34

Dilatace času

#2 24. 08. 2012 10:38 — Editoval Mirgeee (24. 08. 2012 10:43)

Re: Dilatace času

#3 24. 08. 2012 11:06 — Editoval TomF (24. 08. 2012 11:08)

Re: Dilatace času

#4 24. 08. 2012 12:54

Re: Dilatace času

Zápatí