Matematické Fórum

Mirgeee · 29. 08. 2012 23:13

Hmotný bod se pohybuje po logaritmické spirále konstantní úhlovou rychlostí omega, která má polární souřadnice $R = Ae^{b\varphi}$ , kde A a B jsou konstanty > 0. Jaká je závislost změny velikosti zrychlení v závislosti na R?

Je pravda, že se dá snadno odvodit (mechanickou derivací), že
$a_R = \frac{d^2 R}{dt^2} - R\omega^2$
a
$a_\varphi = \frac{1}{R} \frac{d}{dt}(R^2\omega)$
a potom
$a = \sqrt{a_R ^2 + a_\varphi^2}$ ,
kde a_R je zřejmě zrychlení ve směru R a a_\varphi je složka zrychlení k němu kolmá.

A nedalo by se to taky řešit tak, že
$a = \sqrt{g ^2 + a_C^2 + a_R^2}$ ,
kde a_C je Coriolisovo zrychlení $a_C = -2\omega ×v$ ?
Když ne, proč?

medvidek

↑ Mirgeee:
Takové řešení je možné. Gravitační zrychlení $g$ s tím nesouvisí, není ani v zadání, tak bych ho sem netahal.
Mělo by nám vyjít
$a_{\varphi} + a_c = 0$

Tebou uvedené zrychlení $a_{\varphi}$ lze dále upravit, po dosazení za $R$ a provedení derivace bude:
$a_{\varphi}= 2 b \ \omega^2 R$

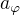Podobně jako pro $a_R$ a $a_\varphi$ lze ("mechanickou derivací") odvodit vztahy pro $v_R$ a $v_{\varphi}$ :
$v_R = \frac{d R}{dt}$
$v_{\varphi}= \omega R$

Pro Coriolisovo zrychlení platí následující vztah, kde čárkami u rychlostí vyjádřujeme skutečnost, že tyto rychlosti jsou měřeny vzhledem k rotující soustavě:
$a_C = -2\omega ×v^\prime = -2\omega × (v_R^\prime + v_{\varphi}^\prime )$
Je evidentní, že $v_{\varphi}^\prime = 0$ , protože hm. bod má úhlovou rychlost právě $\omega$ ,
a také by mělo být zřejmé, že $v_R^\prime = v_R$ .
Můžeme tedy $a_C$ upravit:
$a_C = -2\omega × v_R= -2\omega × \frac{d R}{dt}=-2b \ \omega^2 R$

Poznámka 1:
Dovolil jsem si v zápisech nepoužívat označování vektorových veličin, ale je snad jasné, které to jsou.

Poznámka 2:
Určitě jsi chtěl vypočítat "závislost změny velikosti zrychlení v závislosti na R" ?

Matematické Fórum

#1 29. 08. 2012 23:13

Úloha na souřadnice

#2 11. 09. 2012 06:10 — Editoval medvidek (11. 09. 2012 06:13)

Re: Úloha na souřadnice

Zápatí