Matematické Fórum

L1ebeq · 11. 09. 2012 10:50

Zdravím, rád bych se zeptal na pár drobností ohledně intervalů. Pokusím se to podat jasně a výstižně ...ý příklad

Když jsme měli zadán příklad 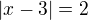$|x-3|=2$ byl výsledek $p=\{1;5\}$

S výpočtem nemám nejmenší problémy, ale zajmalo by mě co představuje písmeno p. Zda je to jen obyčejná proměnná ?

A následně jsme v hodině nedořešili příklad $|x+\pi |>0$ zákonitě vím že pro p platí že je to celá množina R kromě $-\pi$ y ale jak to zapsat ?

Děkuji předem za radu.

nejsem_tonda

To, co u vas znacite $p$ se v literature jmenuje napriklad "obor pravdivosti". Nejedna se o promennou, jedna se o mnozinu cisel, ktera vyhovuji prislusne rovnici nebo nerovnici.

Mimochodem jinde jsem videl napriklad znaceni pro obor pravdivosti $K$ . Asi neexistuje nejaka prisne dodrzovana konvence.

Edit (doplneni odpovedi) Zapis vypada v podstate tak, jak rikas, tj. $p=\mathbb{R}\setminus\{-\pi\}$

L1ebeq · 11. 09. 2012 11:08

↑ nejsem_tonda:

Děkuji za vysvětlení :-) Už jsem opět o něco chytřejší.

Ted jen zjistit jak zaznamenat ten výsledek :-)

zdenek1 · 11. 09. 2012 13:35

↑ L1ebeq:
Doplnění, protože jsi dotaz nazval "intervaly"

dá se to zapsat taky pomocí intervalů jako $p=(-\infty;-\pi)\cup(-\pi;\infty)$

L1ebeq · 11. 09. 2012 13:48 — Editoval L1ebeq (11. 09. 2012 13:49)

↑ zdenek1:

No to je pravda jen jsem trochu bádal a je správné tvrzení 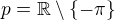$p=\mathbb{R}\setminus \{-\pi \}$ ?

Koukám na výše uvedenou opravenou odpověd a vidím že je to správně děkuji :-)

Matematické Fórum

#1 11. 09. 2012 10:50

Intervaly

#2 11. 09. 2012 10:59 — Editoval nejsem_tonda (11. 09. 2012 11:14)

Re: Intervaly

#3 11. 09. 2012 11:08

Re: Intervaly

#4 11. 09. 2012 13:35

Re: Intervaly

#5 11. 09. 2012 13:48 — Editoval L1ebeq (11. 09. 2012 13:49)

Re: Intervaly

Zápatí