Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 09. 2012 17:13
- Matthias
- Místo: -
- Příspěvky: 72
Funkce
Je dána funkce:
Určete souřadnice jejich průsečíků s osami. Zapište jejich definiční obor a obor hodnot. Zapište intervaly, na kterých funkce roste nebo klesá. Zjistěte, zda je funkce prostá, omezená, sudá nebo lichá.
Můžu se zeptat, jak se postupuje? Děkuji...
Berte na mě ohledy, jsem na matematiku prostě úplně blbej :D
Offline
#2 17. 09. 2012 17:32
#3 17. 09. 2012 17:35
#4 17. 09. 2012 17:50 — Editoval elypsa (17. 09. 2012 18:03)
Re: Funkce
↑ Matthias:
Souřadnice průsečíku: pro průsečík s osou x dosadíme za y 0. Pro průsečík s osou y dosadíme zase za x 0.
Definiční obor=podmínky. Ve zlomku nesmí být nula.
Obor hodnot a další zbylé vlastnosti získáme z grafu.
Před tím než budem schopni nakreslit, musíme to trochu upravit.
Jak na to:
realisticky.cz úprava předpisu lin. lomené
V našem případě se dostaneš na: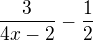
Tohle jsme už schopni hodit na papír, respektive zjistit střed asymptot a nějak ten graf načrtnout.
Střed asymptot bude tedy ![$[0,5;-0,5]$](/mathtex/8f/8fb3e3541f2be06d3d7160e7d292e33e.gif "kopírovat do textarea")
Zvládneš to načrtnout? Dokážeš už podle obrázku najít obor hodnot? Omezenost? Jinak lineární lomená funkce je lichá - souměrná podle počátku..
Jinak intervaly, kde funcke klesá a kde zase roste, jde taky krásně zjistit z obrázku. Stačí si jen uvědomit střed asymptot..
Baf!
Offline
#7 17. 09. 2012 18:26
- Matthias
- Místo: -
- Příspěvky: 72
Re: Funkce
↑ elypsa:
Hmm.. asi to budu potřeboval ještě více polopatě.
pro průsečík s osou x dosadíme za y 0. Pro průsečík s osou y dosadíme zase za x 0.
Tuhle větu vůbec nechápu... To mám udělat jako bod do nuly prostě? Proč?
Co se týče odkazu, cos poslala, ten taky moc nepobírám...
Jak vytvořil z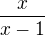 
rovnici 
taky moc nechápu. Konkrétně kde se x-1 vzalo ještě jednou...
A už vůbec nechápu, jak z výsledku ví, co má načmárat do toho grafu...
Slovo asymptot jsem nikdy neslyšel...
Celkově nevím :D
Berte na mě ohledy, jsem na matematiku prostě úplně blbej :D
Offline
#8 17. 09. 2012 19:10 — Editoval smatel (17. 09. 2012 19:14)
Re: Funkce
↑ Matthias:
Hledáme průsečíky s osou x: Každý bod, který leží na ose x má ypsilonovou souřadnici nula.
My hledáme průsečík funkce s osou, tedy konkrétní bod z těchto mnoha bodů na ose. Průsečík je bodem funkce, musí pro něj tedy platit rovnost daná funkcí. Dosadíme tedy do funkce za y nulu a vypočítáme x. Průsečík zapíšeme jako ![$P_x[x;0]$](/mathtex/ed/edfddb392325a476b3e78ff3824a3559.gif "kopírovat do textarea")
, kde x bude to, co jsme vypočítali.
Analogicky pro průsečík 
.
K tomu tvoření - lze to provést takovýmto fíglem:
Offline