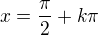Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 28. 09. 2012 17:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Příklad
Zdravím,
ještě nezapomenout na podmínky. Ovšem přechod od  dál - Tvůj návrh ne jest ideál :-)
dál - Tvůj návrh ne jest ideál :-)
Kolega Zdeněk by udělal toto:  (*1/2)
(*1/2) a využil vzorec:
a využil vzorec: 
 já bych podělila (sin(x)) jelikož už jsi takovou úpravu provedl.
já bych podělila (sin(x)) jelikož už jsi takovou úpravu provedl.
Může být? Děkuji.
Offline
#3 28. 09. 2012 18:33
Re: Příklad
To je pravda, tvůj nápad je lepší než můj :-)
Forum občas používám pro své spolužáky, kteří po internetu chtějí něco vysvětlit, tak to napíšu sem a pošlu odkaz :) Je to asi nejlepší, co se dá udělat :)
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#4 28. 09. 2012 21:02
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Příklad
↑ Alivendes:
nápad kolegy Zdeňka je ještě lepší (nevyžaduje stanovení podmínek). Jinak umocnění/odmocnění je neekvivalentní úprava, proto by byla potřeba zkoušky, což v případě goniometrických funkcí není pohodlné.
Je to asi nejlepší, co se dá udělat :)
je to pohodlné, ještě můžeš označovat téma za vyřešené. Děkuji.
Offline