Matematické Fórum

etchie · 29. 09. 2012 21:48

mám príklad výroku, o ktorom je potrebné rozhodnúť o jeho pravdivosti

$(\forall x \in \mathbb{R}) (\exists y \in \mathbb{R}) (x^2+y^2>0)$ (1)

aby sa rozhodovanie zjednodušilo, tak výrok znegujeme:

$(\exists x \in \mathbb{R}) (\exists y \in \mathbb{R}) (x^2+y^2\le0)$ (2)

výrok (2) je určite pravdivý pre x=0, y=0. v tejto forme stačí na dôkaz pravdivosti nájsť jeden vyhovujúci prípad. keďže (2) je negáciou (1), tak potom (1) je nepravdivý.

toľko hovoria moje (možno nepresné) poznámky z prednášky.
teraz otázky:
1. prečo pri negácii sú negované iba $(\forall x \in \mathbb{R})$ a $(x^2+y^2>0)$ ale $(\exists y \in \mathbb{R})$ ostane nedotknuté ?
2. za predpokladu, že negácia je správna, akceptujem, že (2) je pravdivý. keď si ale samostatne vyhodnocujem (1) v pôvodnom tvare, tak mi stále vychádza, že aj (1) je predsa pravdivý. či už je x záporné alebo kladné, tak jeho mocnina je kladná a teda vačšia ako 0. na y vtedy nezáleží. ak je x=0, tak existuje aspoň jedno y, pre ktoré tvrdenie platí. vlastne tých y je celá množina R okrem nuly.

ďakujem za radu

Oxyd · 29. 09. 2012 22:16

Přijde mi to znegované špatně.

Ostatně i závěr mi přijde špatný. Dokazuju (1), mám dáno 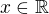$x \in \mathbb{R}$ a abych formuli dokázal, potřebuju najít $y \in \mathbb{R}$ takové, že $x^2 + y^2 > 0$ . Když se mi povede takové y najít pro naprosto libovolné x, tak mám dokázáno. Když teda x je různé od nuly, tak si vyberu y := x a mám $x^2 + y^2 = x^2 + x^2 = 2x^2 > 0$ , protože $x^2 > 0$ , díky tomu, že teď předpokládám, že x je nenulové. No a když je x nula, tak vyberu třeba y := 1 a mám $x^2 + y^2 = 0^2 + 1^2 = 1 > 0$ . Tím jsem tedy našel fungující y pro nenulové x i pro nulové x, tedy jsem našel y pro každé x, a tím jsem dokázal, že (1) platí.

etchie · 30. 09. 2012 18:43

↑ Oxyd:

ďakujem za odpoveď. mám to zle zapísané v poznámkach.
už v tom mám jasno.

Matematické Fórum

#1 29. 09. 2012 21:48

výroky s kvantifikátormi

#2 29. 09. 2012 22:16

Re: výroky s kvantifikátormi

#3 30. 09. 2012 18:43

Re: výroky s kvantifikátormi

Zápatí