Matematické Fórum

utopenveskriptech · 03. 10. 2012 22:58

Dobrý večer,

mám tu zadání (přesněji vysvětlení zadání, protože jsem se jí ptal co mám vlastně dělat), které mi poslala profesorka. Omlouvám se za případné nedostatky ale je to vše co mám a předem děkuji za pomoc.

Dobrý večer,
jde o to odvodit součtový vzorec pro cos (3 alfa) pomocí sin alfa a cos alfa s použitím Eulerova zápisu komplexního čísla

Alivendes · 03. 10. 2012 23:00

Zdravím, neměla na mysli Moiverovu větu a goniometrický tvar komplexního čísla ?

utopenveskriptech · 03. 10. 2012 23:12

má to něco společního s $\mathrm{e}^{i*\varphi}$ = (cos(φ) + i*sin(φ)) ale můžeš mi zkusit nastínit jak by se to počítalo s Moiverovou větu a gon. tvar?

Oxyd · 04. 10. 2012 02:44

Tady se skutečně bude víc hodit ten Eulerův tvar, spíš než goniometrický.

To odvození je takové hezké a jednoduché, je to takový tríček. Abych tě trošku nakopl, zamysli se nad hodnotou $\left(\mathrm{e}^{i\alpha}\right)^3$ . Můžeš ji rozepsat dvěma způsoby – neboli najít rovnosti $\left(\mathrm{e}^{i\alpha}\right)^3 = \text{cosi}$ a $\left(\mathrm{e}^{i\alpha}\right)^3 = \text{cosi jiného}$ . Z toho pak plyne i $\text{cosi} = \text{cosi jiného}$ , a z toho dostaneš vzoreček jak pro $\cos 3\alpha$ , tak dokonce i pro $\sin 3\alpha$ .

Je to trošku hádanka. :) A ano, souvisí to s rovností $\mathrm{e}^{i\alpha} = \cos \alpha + i\sin\alpha$ .

Honzc · 04. 10. 2012 06:58

↑ utopenveskriptech:
Moievrova věta $(cos\;\alpha +i\;sin\;\alpha )^{n}=cos\;n\alpha +i\;sin\;n\alpha$
Eulerův vztah $e^{i\;n\alpha }=cos\;n\alpha +i\;sin\;n\alpha$
ale také platí $(e^{i\;\alpha})^{n}=cos\;n\alpha +i\;sin\;n\alpha$ a $(e^{i\;\alpha})^{n}=e^{i\;n\alpha}$
Vidíš, že je to hodně podobné.
Pak $(\cos\alpha+i\;\sin \alpha)^{3}= \cos3\alpha+i\;\sin 3\alpha$
Levou stranu normálně umocníš podle vzorce $(a+i\;b)^{3}=a^{3}+3ia^{2}b+3i^{2}ab^{2}+i^{3}b^{3}$
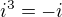nezapomeneš, že $i^{2}=-1$ a $i^{3}=-i$ a dáš k sobě reálné části a imaginární části
Ty potom provnáš s reálnou částí a imagiární částí pravé strany.
(Pokud máš udělat jen $\cos 3\alpha$ stačí porovnat pouze reálné části)

Alivendes · 04. 10. 2012 14:24

Ano, to je důkaz pomocí moiverovi věty jak jsem psal. Nevidím důvod údávat exponenciální tvar komplexního čísla.

utopenveskriptech

pokud jsem pochopil správně zadání pí. profesorky tak je cílem vyjádřit cos3\alpha.

1. krok

$cos3\alpha + isin3\alpha = (cos\alpha + isin\alpha )^{3}$

2. krok

$cos3\alpha + isin3\alpha = cos^{3}\alpha + 3cos^{2}\alpha isin\alpha + 3cos\alpha sin^{2}\alpha - isin^{3}\alpha$

3. krok

$cos3\alpha -cos^{3}\alpha - 3cos\alpha sin^{2}\alpha = 3cos^{2}\alpha isin\alpha - isin^{3}\alpha - isin3\alpha$

a dále pak nevím co s tím. sorry -_-

jelena · 04. 10. 2012 22:46

↑ utopenveskriptech:

Zdravím,

od 2. kroku porovnat "reálné nalevo = reálné napravo" (a také imaginární levo=pravo, ale to není potřeba pro konkrétní důkaz).

Jinak zadáním klíčových slov najdeš hodně důkazů, např. i rovnou na Wikipedie.

kolega Oxyd napsal(a):
Je to trošku hádanka. :)

mně se nepodařilo vyluštit, děkuji :-)

Honzc · 05. 10. 2012 05:53

↑ utopenveskriptech:
Ještě, že jsem ti psal "...nezapomeneš, že $i^{2}=-1$ " a ty ve druhém kroku ve třetím členu pravé strany klidně mrskneš místo mínus plus.
Pak porovnáš:
Re: $cos3\alpha= cos^{3}\alpha- 3cos\alpha sin^{2}\alpha$

Matematické Fórum

#1 03. 10. 2012 22:58

Komplexní čísla - euleruv zápis komplexního čísla

#2 03. 10. 2012 23:00

Re: Komplexní čísla - euleruv zápis komplexního čísla

#3 03. 10. 2012 23:12

Re: Komplexní čísla - euleruv zápis komplexního čísla

#4 04. 10. 2012 02:44

Re: Komplexní čísla - euleruv zápis komplexního čísla

#5 04. 10. 2012 06:58

Re: Komplexní čísla - euleruv zápis komplexního čísla

#6 04. 10. 2012 14:24

Re: Komplexní čísla - euleruv zápis komplexního čísla

#7 04. 10. 2012 20:58 — Editoval utopenveskriptech (04. 10. 2012 20:58)

Re: Komplexní čísla - euleruv zápis komplexního čísla

#8 04. 10. 2012 22:46

Re: Komplexní čísla - euleruv zápis komplexního čísla

kolega Oxyd napsal(a):

#9 05. 10. 2012 05:53

Re: Komplexní čísla - euleruv zápis komplexního čísla

Zápatí