Matematické Fórum

↑ Fuckiers:
Na to jsou zde nástroje
První
Druhý

↑ Alivendes:
A co brání studentům na střední škole, aby si vzali třeba čtverečkovaný papír, udělali si tabulku o dvou řádcích (x a y) a postupně si počítali podle předpisu funkce "body" grafu.
To je zvolili si x a k tomu vypočítali y a dali jako jeden sloupeček do tabulky.
Takto to udělali pro "několik" x a spočítaných y (pokud je ve funkci nějaké dělení obsahující x nezapomněli popřemýšlet jaké hodnoty nabude y, když výraz ve jmenovateli bude 0) a potom jednotlivé sloupečky (body) vynesli do grafu a ty potom spojili hladkou čárou (respektive několika hladkými čarami).

↑ jelena:

Přesně tak, my jsme také museli grafy posouvat.

↑ Fuckiers:
Zdravím,

abych se přidal, i my jsme museli grafy posouvat atd. Počítat body je naprostá hloupost (u polonymu pátého řádu bych byl vážně zvědavý, jak by se takový graf konstruoval)... Tedy bych rád vzkázal autorovi, že bude-li mu někdo radit podobnou věc, ať ho rovnou kopne do příslušných míst...

Nicméně, přijde mi, že dotaz zůstal úplně nezodpovězen...

No, jak radil Alivendes ke grafu první funkce, je třeba vědět, jak vypadá funkce . Všechny grafy mají určitá pravidla pro jejich posouvání, uzavírání se atd. Já ti sem můžu napsat, jak bych podobnou věc řešil já.

Mám předpis funkce . Předně bych si přepsal tento předpis tak, abych měl jako první výraz s . Tohle není žádná nutnost, ale pro vysvětlení zde se to bude hodit. Dostanu tedy výraz:



No a přesně v tuto chvíli přichází na věc graf funkce . Tento graf se zkontruuje (netušíš-li jak, na konci mého příspěvku k tomu bude pár poznámek).

Tento graf však ještě není náš chtěný graf. Nyní se zaměříme na . Tento předpis znamená, že graf, který už máme, posuneme doprava nebo doleva o jedničku. Jak to ale udělat? No, Vězměne si určitý bod 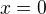. Tento bod není definovaný pro první graf. Pro druhý graf nebude definovaný bod 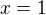, že? Tedy graf se posnue o jedničku doprava (abychom bod, kterým neprochází funkce, měli v jedničce).

A co dál? Inu, před celou závorkou máme mínus: . To znamená, že z každé záporné hodnoty uděláme kladnou a z každé kladné zápornou. Jelikož máme pouze kladné hodnoty, dostaneme graf, kde budou samé záporné hodnoty. A jak přesně graf nakreslit? Musí být s tím minulým symetrický podle osy x (tak chápeme znaménko mínus - jako symetričnost podle osy x).

Poslední krok je přičtená jednička (proto jsem ji psal nakonec): . To už bude náš výsledný graf funkce. Vezmeme tedy náš poslední graf a ke každému bodu přičteme jedničku - tj. posuneme ho o 1 vzhůru. Tím jsme dostali finální graf, který jsme chtli nakreslit.

========
Ohledně 1/x^4

Skrytý text:

Kdybys netušil, jak nakreslit graf , potom postupuj následovně: Určitě víš, jak vypadá graf funkce . Je to hyperbola, kterou ti ukáži na obrázku.


Je zřejmé, že funkce bude vypadat podobně. Bude akorát více "zahnutá" a ze záporných hodnot se stanou kladné (funkce je sudá). Viz tedy následující obrázek:


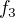Všechny ostatní funkce už budou podléhat stejným pravidlům a bude platit, že pro sudou mocninu ve jmenovateli budou vypadat jako funkce a pro budou vypadat jako 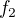. Jediné, co bude rozdílné bude "sevření". Na následujícím obrázku vidíš rozdíl mezi 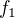a . ( je modře)

.