Matematické Fórum

Aikido21 · 07. 10. 2012 22:16 — Editoval jelena (08. 10. 2012 00:02)

Cavte,
chcel by som vas poziadat o pomoc s tymto prikladom. Predpokladam, ze je to limita s typom neurcitosti 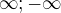$\infty; -\infty$ a tak ju treba rozsirit vhodnou jednotkou na typ 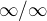$\infty /\infty$ ...a tu je moj problem, ze neviem ako to spravit...samozrejme, ze nejake vlastne kroky vypoctu mam ale zda sa mi zbytocne ich sem prepisovat...

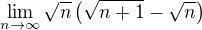$\lim_{n \to \infty} \sqrt{n}\left ( \sqrt{{n+1}}-\sqrt{n} \right )$ (aby vam to zobrazilo spravne, mozete vyskusat http://www.codecogs.com/latex/eqneditor.php)

Dakujem za pomoc

jelena · 08. 10. 2012 00:06

Zdravím,

(aby vam to zobrazilo spravne, mozete vyskusat http://www.codecogs.com/latex/eqneditor.php)

opravila jsem zápis pomocí tlačítka TeX pod oknem zprávy (+ drobné úpravy).

Rozšířit 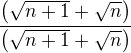$\frac{\left ( \sqrt{{n+1}}+\sqrt{n} \right )}{\left ( \sqrt{{n+1}}+\sqrt{n} \right )}$ a na závěr vytknout v jmenovateli $\sqrt{n}$ .

Téma jsem však našla již označené za vyřešené, tak nevím, zda je aktuální.

Matematické Fórum

#1 07. 10. 2012 22:16 — Editoval jelena (08. 10. 2012 00:02)

Limita s vhodnou jednotkou

#2 08. 10. 2012 00:06

Re: Limita s vhodnou jednotkou

Zápatí