Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » zlomek jako součet převrácených hodnot různých celých čísel (TOTO TÉMA JE VYŘEŠENÉ)
#1 22. 11. 2008 10:29
zlomek jako součet převrácených hodnot různých celých čísel
ahoj, mám za úkol najít algoritmus který převede zlomek do tvaru v nadpisu... například 4/5 = 1/2 + 1/4 + 1/20... Alogoritmus má tedy převést zlomek p/q kdy 1<p<q... Už nad tím přemýšlím druhý den, dokonce i v pátek:), a nic mě nenapadlo...díky za rady...
Offline
#2 22. 11. 2008 11:47
Re: zlomek jako součet převrácených hodnot různých celých čísel
V podstatě mně už něco napadlo a mohlo by to fungovat.
Vezmu příklad  .
.
Určím si první sčítanec, například  . Vím, že k
. Vím, že k  musím přičíst ještě
musím přičíst ještě 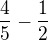 abych dostal celkem ony
abych dostal celkem ony  .
.
Takže 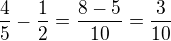 .
.
Dostávám tedy, že 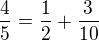
My ale vyžadujem, aby v čitateli byla 1. Proto si určím další sčítanec, který od  odečtu, ale pozor, musí být menší. Takže volím
odečtu, ale pozor, musí být menší. Takže volím  a počítám
a počítám 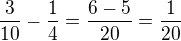
a jsem u konce, konečný výpočet je tedy 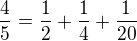 .
.
Další příklad:
Volím zlomek 
Opět volím první sčítanec (nižší)  a počítám
a počítám 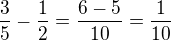 a jsem hned u konce.
a jsem hned u konce.
Konečný výsledek je tedy 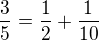
Další příklad:
Volím 
Volím první sčítanec  a počítám
a počítám 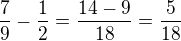 opět ale vyžadujem ,aby v čitateli byla 1, proto volím další sčítanec
opět ale vyžadujem ,aby v čitateli byla 1, proto volím další sčítanec  (1/3 nelze, protože je větší než 5/18 a algoritmus je dán tak, že sčítanec musí být menší).
(1/3 nelze, protože je větší než 5/18 a algoritmus je dán tak, že sčítanec musí být menší).
Počítám 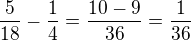 a jsem u konce.
a jsem u konce.
Konečný výsledek je 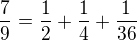 .
.
Zřejmě to funguje, takže jsem takový algoritmus našel.
oo^0 = 1
Offline
#3 22. 11. 2008 11:53 — Editoval ttopi (22. 11. 2008 11:57)
Re: zlomek jako součet převrácených hodnot různých celých čísel
Další příklad:
Počítám 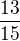

Abych to srhnul, volíme si postupně menší a menší sčítance tak, abychom skončili tím, že vyjde 1/něco a pak všechny ty sčítance sečtem a máme původní zlomek.
oo^0 = 1
Offline
#6 22. 11. 2008 12:05
Re: zlomek jako součet převrácených hodnot různých celých čísel
Protože začínám prostě od nejmenšího možného zlomku :-)
Ale pozor, jak jsem řekl, první sčítanec musí být menší než zlomek, který vyjadřuješ.
Takže třeba pro  nemůže být první sčítanec
nemůže být první sčítanec  ale něco, co je menší než
ale něco, co je menší než 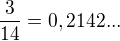 takže třeba
takže třeba  by byl prvním sčítancem. A tenhle příklad si schválně zkus dodělat, co ti vyjde :-)
by byl prvním sčítancem. A tenhle příklad si schválně zkus dodělat, co ti vyjde :-)
oo^0 = 1
Offline
#7 22. 11. 2008 12:06
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ leniczka:Samozřejmě, protože jsem ho nedělal podle svého algoritmu, ale už jsem ho smazal :-)
oo^0 = 1
Offline
#8 22. 11. 2008 12:13
Re: zlomek jako součet převrácených hodnot různých celých čísel
OK, já nad tím přemýšlím dva dny a ty to máš za pět minut:) Asi fakt Einstein:)
Jinak těch 3/14... První sčítanec je 1/5... 3/14 - 1/5 je 1/70. Takže 3/14 = 1/70 + 1/5. Fakt fo funguje, díky moc:)
Offline
#9 22. 11. 2008 12:14
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ leniczka:
V žádném případě, Einsteini jsou tu jiní (BrozekP, Pavel, Marian, Kondr - namátkou)...
Super, máš to správně :-)
oo^0 = 1
Offline
#10 22. 11. 2008 12:17
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: zlomek jako součet převrácených hodnot různých celých čísel
ttopi napsal(a):
Zřejmě to funguje, takže jsem takový algoritmus našel.
Algoritmus by měl být konečný. Můžeš tedy ukázat, že dříve nebo později pro každý zlomek algoritmus skončí? (Příklady, které fungují mě nepřesvědčí :-) )
Offline
#11 22. 11. 2008 12:26
Re: zlomek jako součet převrácených hodnot různých celých čísel
No od čísla x/y když postupně budeš ubírat a ubírat čísla ve tvaru 1/z, tak jednou musíš skončit na 0, protože x/y lze vyjádřit v desetinném čísle a 1/z také. Pokud budu ubírat od čísla 0,6 třeba pořád 0,1 tak skončím na 0 určitě.
Já bych spíš použil oblíbenou větu většiny učitelů - Tvrdíš snad, že to nefunguje? Tak mi to své tvrzení dokaž :-)
oo^0 = 1
Offline
#12 22. 11. 2008 12:39
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ ttopi:Když budu od zlomku 1/1 odebírat 1/2, 1/4, 1/8,.... tak nikdy neskončím. To sice není případ tvého algoritmu, ale chtělo by to zdůvodnit.
Řečeno jinak: Nejde argumentovat tím, že se zmenšuje hodnota zlomku. Musí se v každém kroku zmenšvat něco, co se může zmenšit jen konečně-krát, třeba p, q, p+q, p*q,....
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#13 22. 11. 2008 12:41
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ Kondr:
V zadání je ale 1<p<q.
Chtělo se najít algoritmus, byl nalezen, kdo tvrdí, že nefunguje, ať udá jeden příklad čísel p a q, kde 1<p<q , pro která to neplatí :-)
oo^0 = 1
Offline
#14 22. 11. 2008 12:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ ttopi:
Zajímavý přístup, proč se vlastně lidé zabývali důkazem Velké Fermatovy věty? Stačilo říct "Ukažte mi čísla, která ji vyvrací! Nemáte? Tak věta platí." :-)
Offline
#15 22. 11. 2008 13:08
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ BrozekP:
Děláš z komára velblouda. Úkolem bylo nalézt algoritmus a nic víc. Pro mě zřejmě funguje, pokud pro tebe ne, zkus si důkaz udělat sám :-)
oo^0 = 1
Offline
#16 22. 11. 2008 16:01
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: zlomek jako součet převrácených hodnot různých celých čísel
Myslím, že jsem našel důkaz, že algoritmus je správný. Zatím ho zde nebudu uvádět, řekl bych, že není příliš těžký, takže by si ho myslím mohl zkusit i lukaszh a ostatní, kdo rádi dokazují a úlohy na důkazy co se tu objevují jsou pro ně příliš těžké.
Offline
#17 19. 01. 2009 17:11
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ BrozekP:
Po téměř dvou měsících se vracím k tomuto tématu a uvedu svůj postup důkazu:
Máme tedy čísla 1<p<q.
a) Pokud p dělí q, pak jednoduše 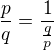 je hledaný rozklad.
je hledaný rozklad.
b) Pokud p nedělí q, pak jistě exisuje 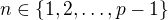 takové, že p dělí
takové, že p dělí 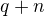 . Platí tedy
. Platí tedy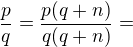
čitatel i jmenovatel je dělitelný p, budu proto krátit p a stále budu mít v čitateli a jmenovateli přirozená čísla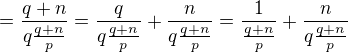
Rozložil jsem tedy zlomek  na součet zlomku s čitatelem 1 a zlomku s čitatelem menším než p. Protože
na součet zlomku s čitatelem 1 a zlomku s čitatelem menším než p. Protože ,
,
můžu na druhý zlomek použít stejný postup rozkladu. Protože je čitatel n menší než p, pak tento postup budu opakovat nejvýše p krát a pak se určitě dostanu na n=1 a mám tedy požadovaný rozklad. Tento postup také zajišťuje, že se v rozkladu nebudou opakovat stejní jmenovatelé (protože  , je druhý zlomek
, je druhý zlomek 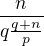 menší než první
menší než první 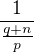 )
)
Offline
#18 19. 01. 2009 17:24 — Editoval musixx (19. 01. 2009 17:27)
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ BrozekP: Rekl bych, ze timto jsi dokazal, ze nejaky takovy soucet existuje. Podle me jsi ale nedokazal, ze kdyz pouziju postup od ttopi (ktery vzdy jako dalsi scitanec bere nejvetsi mensi 1/x nez je aktualni zbytek), tak ze skoncim. Nebo se pletu?
Offline
#19 19. 01. 2009 17:58
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: zlomek jako součet převrácených hodnot různých celých čísel
↑ musixx:
Pokud bych nevzal zlomek 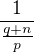 ale zlomek s o jedna menším jmenovatelem
ale zlomek s o jedna menším jmenovatelem 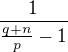 , tak platí (použiju
, tak platí (použiju  )
) .
.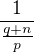 je tedy největší zlomek s čitatelem 1 menší než
je tedy největší zlomek s čitatelem 1 menší než  .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » zlomek jako součet převrácených hodnot různých celých čísel (TOTO TÉMA JE VYŘEŠENÉ)