Matematické Fórum

Frantik88

Najděte maximální intervaly monotonie, lokální extrémy

$f(x) = x \cdot (x^2-3)$

Df = R
Nulové body: 0 a odmocnina(3)

f(x)' = 3x^2 - 3
Stacionární body: xs1 = 1 a xs2 = -1

f(x)''=6x-3
f(xs1)'' = 3 > 0 - xs1 ostré lokální minimum
f(xs2)'' = -9 < 0 - xs2 ostré lokální maximum

konvexita grafu: (0, +oo)
konkávnost grafu: (-oo; 0)

Je tomu tak?

Pavel Brožek · 22. 11. 2008 14:24

Je to polynom stupně tři, takže bude mít dva nebo žádný lokální extrém, extrémy rozdělí R na intervaly monotonie. Extrémy určíš z derivace. Kde konkrétně je problém?

Pavel Brožek

↑ Frantik88:

Máš špatně druhou derivace (derivace konstanty). Pak ti chybí jeden kořen: 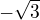$-\sqrt3$

Konvexitu a konkavitu máš dobře, jak jsi ji určil, když máš špatně druhou derivaci?

Frantik88 · 22. 11. 2008 14:33

Asi nahoda...

f(x)''=6x
f(xs1)'' = 3 > 0 - xs1 ostré lokální minimum
f(xs2)'' = -3 < 0 - xs2 ostré lokální maximum

Matematické Fórum

#1 22. 11. 2008 14:21 — Editoval Frantik88 (22. 11. 2008 14:25)

Najděte maximální intervaly monotonie, lokální extrémy

#2 22. 11. 2008 14:24

Re: Najděte maximální intervaly monotonie, lokální extrémy

#3 22. 11. 2008 14:28 — Editoval BrozekP (22. 11. 2008 14:30)

Re: Najděte maximální intervaly monotonie, lokální extrémy

#4 22. 11. 2008 14:33

Re: Najděte maximální intervaly monotonie, lokální extrémy

Zápatí