Matematické Fórum

pepa999 · 30. 06. 2011 12:23

Dobrý den, jak by se řešila tato rovnice?

$\sin x + \sin 3x = \sin 2x + \sin 4x$
$x \in R$

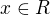
Dostal jsem se až k rovnici,

$16*(\sin x)^6-36*(\sin x)^4+25(\sin x)^2+4=0$

ale nevím jak dál a možná, že jsem někde udělal chybu.

Vím, že tato rovnice není s původní rovnicí ekvivalentní, ale je to
kvůli tomu, že jsem umocňoval na druhou a dělil výrazem $\sin x$

byk7 · 30. 06. 2011 12:32

Asi to půjde s využitím vztahu $\sin(nx)=\frac12\text{i}\text{e}^{-\text{i}nx}-\frac12\text{i}\text{e}^{\text{i}nx}$ a pak to řešit jako exponenciální rovnici.

musixx · 30. 06. 2011 12:48

$\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}2\cos\frac{\alpha-\beta}2$ ,
odkud je původní rovnice ekvivalentní rovnici
$2\sin2x\cos x=2\sin3x\cos x$ .

pepa999

Byk7: Je to příklad z učebnice, ve které nepředpokládají znalost tohoto vzorce, ale pouze základních goniometrických vzorců.

Musixx: Dík, teď už to snad vyřeším.

Alivendes · 30. 06. 2011 13:23

↑ pepa999:
To je asi pravda, tohle je vysokoškolská matematika ↑ byk7: :)

Asi bych se řídil tím, co popsal kolega ↑ musixx:

byk7 · 30. 06. 2011 13:40

↑ Alivendes: ale tak, snad je to taky cesta

musixx · 30. 06. 2011 13:54

↑ byk7: ↑ Alivendes: Jak by se to teda řešilo jako exponenciální rovnice? Jen tak ze zájmu...

byk7 · 14. 10. 2012 00:00

↑ musixx:

no, asi by to nešlo...

Matematické Fórum

#1 30. 06. 2011 12:23

Náročná goniometrická rovnice

#2 30. 06. 2011 12:32

Re: Náročná goniometrická rovnice

#3 30. 06. 2011 12:48

Re: Náročná goniometrická rovnice

#4 30. 06. 2011 12:53 — Editoval pepa999 (30. 06. 2011 12:55)

Re: Náročná goniometrická rovnice

#5 30. 06. 2011 13:23

Re: Náročná goniometrická rovnice

#6 30. 06. 2011 13:40

Re: Náročná goniometrická rovnice

#7 30. 06. 2011 13:54

Re: Náročná goniometrická rovnice

#8 14. 10. 2012 00:00

Re: Náročná goniometrická rovnice

Zápatí