Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz s poslední cifrou čísla (TOTO TÉMA JE VYŘEŠENÉ)
#1 13. 10. 2012 22:39
Důkaz s poslední cifrou čísla
Dobrý den,
řeším následující úlohu. Zjistil jsem, že když budu umocňovat přirozená čísla na třináctou, tak vždy poslední číslice umocněného čísla bude shodná s poslední číslicí mocněného čísla. Chtěl bych se pokusit tuto hypotézu nějakým způsobem dokázat, stačilo by mi pro poslední číslici rovnou devíti.
Věta:
Nechť je  , pak přirozené číslo
, pak přirozené číslo  má ve svém zápisu na posledním místě číslo 9.
má ve svém zápisu na posledním místě číslo 9.
Důkaz jsem zkoušel indukcí podle k, ale zasekl jsem se v druhém kroku:
První krok pro 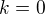 :
:
Druhý krok: má na posledním místě 9, pak má i
má na posledním místě 9, pak má i  na posledním místě 9.
na posledním místě 9.
Pomůže mi někdo pokračovat?
Děkuji.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 13. 10. 2012 22:57
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: Důkaz s poslední cifrou čísla
A nejde to primo? 
Poslednu cifru ovlyvni jenom  zvysok je delitelny 10.
zvysok je delitelny 10.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz s poslední cifrou čísla (TOTO TÉMA JE VYŘEŠENÉ)