Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Def. obor fce - logaritmus, exponenciální a odmocnina ne druhá (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 10. 2012 18:47 — Editoval nika.v (14. 10. 2012 18:50)
Def. obor fce - logaritmus, exponenciální a odmocnina ne druhá
Zdravím lidičky,
jsem se trochu zmátla. Prosím, zkontrolujte mi mou úvahu :-)
Úkolem je načrtnout graf a určit Df u fcí:
y=2log(x-1)
logaritmus je při základu 2, nejde mi to bohužel vložit editorem
bych řekla, že podmínkou k Df je pouze argument větší než nula, tedy x větší než-li 1, ale problém mám s grafem vzhledem k danému základu logaritmu. Bude graf řekněme obdobný klasickému dekadickému logaritmu, kdy protíná osu x v 1, jen bude trochu sklopenější. Hledala jsem v tabulkách, ale nic mě nenakoplo :-(.
y=2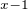 +3
+3
Df všechna reálná čísla y=\sqrt[3]{x-4}$
y=\sqrt[3]{x-4}$
tady bych řekla, že podmínka vše pod odmocninou větší nebo rovno nule už neplatí, že? vzhledem k tomu, že lze nyní odmocnit záporné číslo.
Tudíž graf vypadá, viz. obr. Jinak by byl omezen od čísla 4 směr doprava na ose x.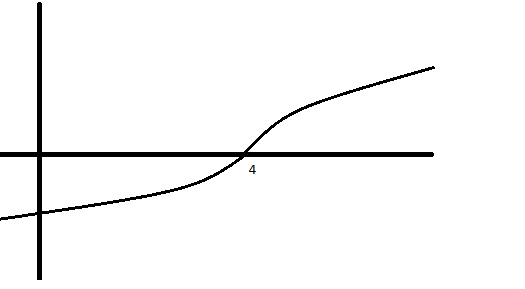
Díky za pomoc, začínám asi blbnout.
Ejunka
Offline
- (téma jako vyřešené označil(a) nika.v)
#3 14. 10. 2012 19:26 Příspěvek uživatele Takjo byl skryt uživatelem Takjo. Důvod: Nesprávná úvaha
#6 14. 10. 2012 19:37
Re: Def. obor fce - logaritmus, exponenciální a odmocnina ne druhá
↑ Takjo:↑ Tomas.P: vy dva nešiřte bludy
Offline
#8 14. 10. 2012 19:52
Re: Def. obor fce - logaritmus, exponenciální a odmocnina ne druhá
↑ Takjo:
Váš definiční obor (příspěvek #3) je prostě špatně (a graf taky). Musíte se ty vzorečky učit celé, i podmínkami platnosti.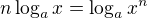 platí pouze, když jsou obě strany definované
platí pouze, když jsou obě strany definované
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Def. obor fce - logaritmus, exponenciální a odmocnina ne druhá (TOTO TÉMA JE VYŘEŠENÉ)

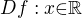

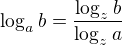 pro libovolné přípustné
pro libovolné přípustné  , tedy logaritmy o různých základech se liší jenom o multiplikativní konstantu
, tedy logaritmy o různých základech se liší jenom o multiplikativní konstantu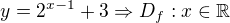
![kopírovat do textarea $y=\sqrt[3]{x-4}\Rightarrow D_{f}:x\in \mathbb{R}$](/mathtex/7a/7a51e3c452e1168ceb84a3ad4291a61f.gif)