Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 10. 2012 10:33 — Editoval Andrejka3 (17. 10. 2012 12:55)
Univerzální prvek
Ahoj,
pomozte mi, prosím, s nalezením univerzálního prvku pofunktoru  funktoru
funktoru 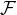 ,
,
kde 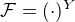 je exponenciální funktor (
je exponenciální funktor ( je nějaká zadaná množina).
je nějaká zadaná množina).
Pro libovolnou množinu  je podfunktor definován
je podfunktor definován 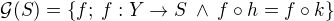 , kde
, kde 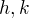 jsou zadané fce
jsou zadané fce 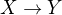 .
.
Našla jsem něco, co by s tím mělo souviset: Wikipedia
Možná to tam je přímo napsané, ale mě to nedochází.
Díky.
Definice:
Univerzální prvek:
Funktor:
Exponenciální funktor:
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 17. 10. 2012 14:34
Re: Univerzální prvek
ahoj, len mala poznamka;
v teorii kategorii, je zvykom representovat situcie vdaka funkcnym diagramom.
Vies ako sa tvoria taketo veci vdaka latexu?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 17. 10. 2012 15:56
Re: Univerzální prvek
↑ vanok:
Ahoj, ano, v latexu používám \xymatrix{}
Chybí mi tam některé druhy šipek, jaký používáš ty?
Jinak, napadlo mě ještě toto:
Volím si libovolnou (neprázdnou) množinu  . Volim
. Volim 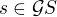 , takže
, takže 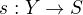 . Pokud je
. Pokud je 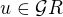 univerzální prvek, pak musí existovat právě jedna
univerzální prvek, pak musí existovat právě jedna 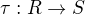 tak, že
tak, že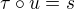 tedy
tedy 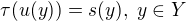 by mě mělo jednoznačně definovat fci
by mě mělo jednoznačně definovat fci 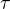 . Tuším, že by mělo být
. Tuším, že by mělo být  , tj. faktorová množina podle jisté ekvivalence, univerzální prvek
, tj. faktorová množina podle jisté ekvivalence, univerzální prvek  pak bude projekce
pak bude projekce  ,
, ![kopírovat do textarea $y \mapsto [y]_{\sim}$](/mathtex/17/170db506702f27c8fb8e879edd757fa6.gif) .
.
Mám problém s definicí té relace  .
.
Vím, že na množině  , (kde
, (kde  je obraz
je obraz  fce
fce  ) jsou jen jednoprvkové třídy
) jsou jen jednoprvkové třídy  , tj.
, tj. ![kopírovat do textarea $y \in Y \setminus (h_*X \cup k_*X) \Rightarrow [y]_{\sim}=\{y\}$](/mathtex/28/283e77d819bb64ae627bb7c1cdb6e761.gif) .
.
Dále, ![kopírovat do textarea $y \in(h_*X \cup k_*X) \Rightarrow [y]_{\sim} \supset \{\tilde{y} \in Y; \; (h(x)=\tilde{y} \wedge k(x)=y) \vee (k(x)=\tilde{y} \wedge h(x)=y )\}$](/mathtex/9b/9bb6214423fa5af2d77cdc840a89347b.gif) . Ale formálně nejsem schopna napsat celý předpis pro tu ekvivalenci.
. Ale formálně nejsem schopna napsat celý předpis pro tu ekvivalenci.
(Značím ![kopírovat do textarea $[y]_{\sim}=\{\tilde{y}; \; \tilde{y} \sim y\}$](/mathtex/66/6688b6961a45024629df67cdd59d072f.gif) )
)
Podívám se na pm a Tvé navržené řešení, snad mé představy výše nebudou úplně mimo.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 17. 10. 2012 16:08 — Editoval Andrejka3 (17. 10. 2012 21:03)
Re: Univerzální prvek
↑ vanok:
Takže to vypadá podle pm, že jsem nešla úplně špatnou cestou. Myslím, že bych to mohla už díky tomu dořešit. Až se tak stane, napíšu zde řešení.
Díky moc!
Edit: vlastně jsem dostala celé řešení, takže jen opíšu zbytek:
Relace  se dostane jako tranzitivní uzávěr relace
se dostane jako tranzitivní uzávěr relace  , kde
, kde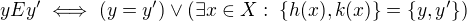 .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
 a
a 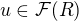 .
.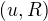 (nebo
(nebo 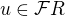 ) je univerzálním prvkem funktoru
) je univerzálním prvkem funktoru ![kopírovat do textarea $(\forall \text{ množina } S)\: (\forall s \in \mathcal{F}S)\: (\exists ! \: h : R \rightarrow S , \; [\mathcal{F}(f)]u=s) \;.$](/mathtex/e4/e4c4d7ceab487d17525e9979b2716060.gif)
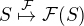
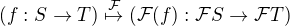 ,
,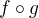 , pak
, pak 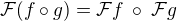 ,
,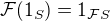 .
.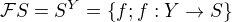 ,
,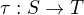 .
. 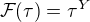 tak, že
tak, že  .
.