Matematické Fórum

liquid · 17. 10. 2012 14:50

ahoj

snazim se vyresit, dle meho, trivialni vec, ale nejak sem se v tom ztratil.

potrebuju spocitat silu, kterou musim udelit telesu, tak aby se pohybovalo po trajektorii o ktere vim: pocatecni bod (x0,y0), pak jeden bod ktery ji nalezi (x1,y1) a pak vim, ze vrchol paraboly je v dvounasobne vysce nez byl byl (x1,y1).

znam tedy x0, y0, x1, y1, g, y2

zde je muj postup reseni, ale ten vede na to, ze mi v rovnici zbyde i "t".

co delam spatne?

diky

jelena · 17. 10. 2012 15:32

↑ liquid:

takovou událost si nemohu nechat ujít.

Předně bych zafixovala bod (x_0, y_0) do počátku souřadnic (tedy 0, 0). Ve Tvém zápisu se mi nepozdává 4. řádek nalevo (pokud $d=(y_1-y_0)$ , potom $2d=\ldots$ ), ale to se odstraní vhodnou souřadnici počátečního bodu.

Pokud jsem neudělala nějakou chybu, tak mám kvadratickou rovnici s neznámou $x_2$ . Bylo to účelem? Děkuji a zdravím :-)

liquid · 17. 10. 2012 16:09

Ahoj!

dnes sem nejak totalne vedle
pokusil sem se to prepocitat, ale me tam proste zbyde "t"...

$x^2$ jeste uplne neni to, co chci, ja se z toho snazim vydolovat $v$ a to jak $v_{x}$ tak $v_{y}$ .

neboli:

Jakky V musim pusobit na teleso v bode A tak, aby proletlo bode B a zaroven proletlo bodem s vyskou 2x vetsi (relativne k trajektorii)?

tady je novy pokus s opravenym 2d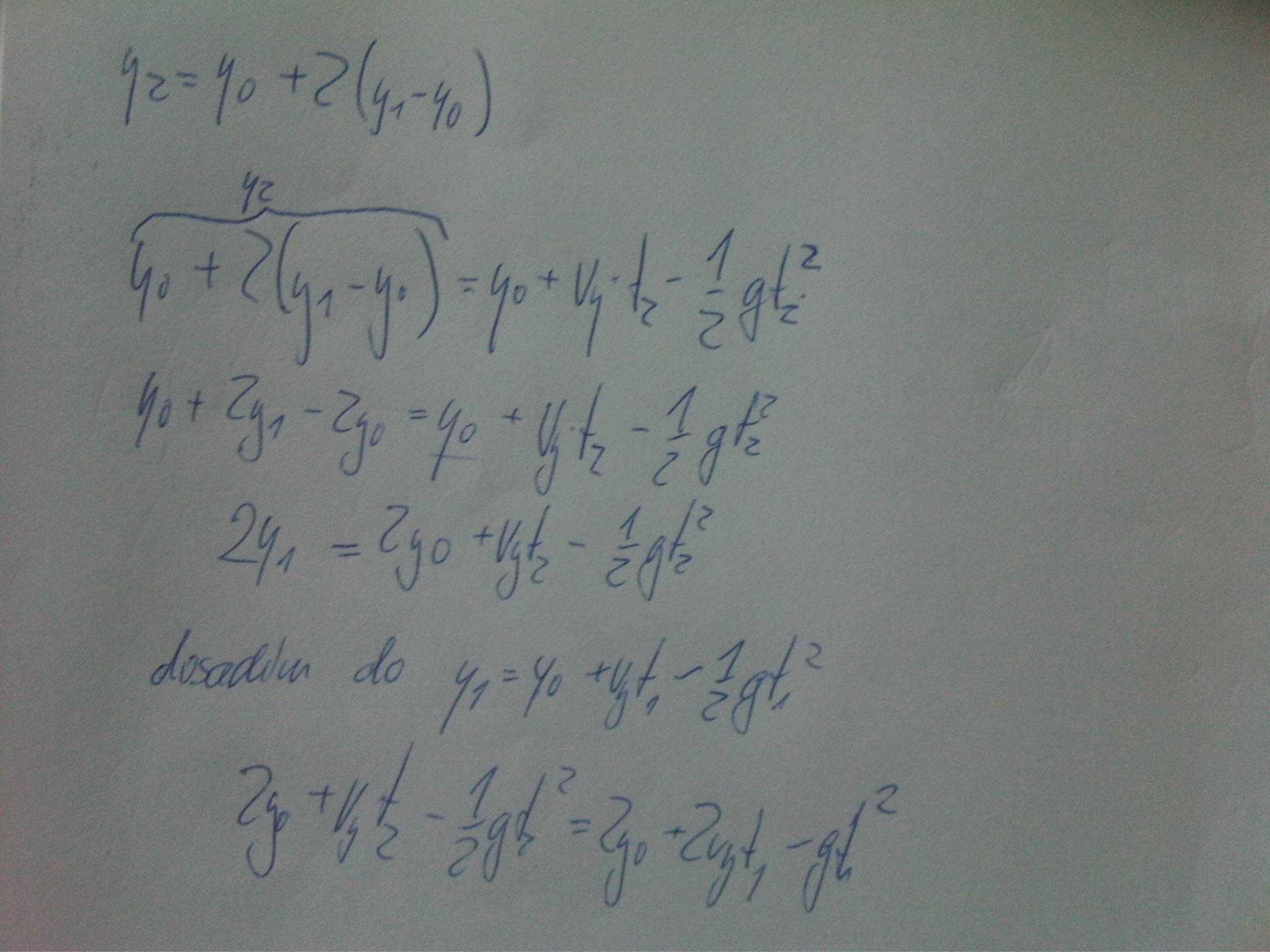

ale zbyva mi tam to same...

liquid · 17. 10. 2012 16:12

aha, ted me tak napada...

ja tam nikde nemam zapocitanyy to, ze ten bod [x_2,y_2] je ve vrcholu trajektorie...
ani z obrazku to neni zrejme, protoze je orizly :)

takhle mam nekonecne moc resenich, prave v zavislosti treba na "t".

jak to tam ale zakomponuju?

zdenek1 · 17. 10. 2012 16:25

↑ liquid:
rovnice trajektorie jsou
$\begin{cases}x=x_0+v_xt\\y=y_0+v_yt-\frac12gt^2\end{cases}$
z první rovnice $t=\frac{x-x_0}{v_x}$ dosadíme do druhé rce
$y=y_0+\frac{v_y}{v_x}(x-x_0)-\frac{g}{2v_x^2}(x-x_0)^2$

a) dosadíme souřednice prvního bodu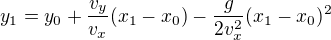
$y_1=y_0+\frac{v_y}{v_x}(x_1-x_0)-\frac{g}{2v_x^2}(x_1-x_0)^2$ (1)

b) Vztah pro maximální výšku šikmého vrhu $H_{max}=\frac{v_0^2\sin^2\alpha}{2g}$ přepíšeme do našich proměnných
$y_v-y_0=\frac{v_y^2}{2g}$ , kde $y_v$ je souřadnice vrcholu paraboly. Podle zadání je $y_v-y_0=2(y_1-y_0)$

dostáváš rovnici
$2(y_1-y_0)=\frac{v_y^2}{2g}$ (2)

Z rovnice (2) vypočítáš $v_y$ , dosadíš do rovnice (1) a určíš $v_x$ .